ML Wiki

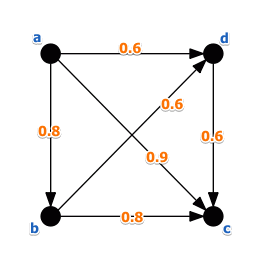
Valued Preference

This is a preference structure for Modeling Preferences in MCDA.

In this case the relation $P$ is not binary

• instead of saying $a \ P \ b$ or $b \ P \ a$ we express the intensity of preference:
• $v(a, b)$ is valued preference of $a$ to $b$
• $v(b, a)$ is valued preference of $b$ to $a$
• 

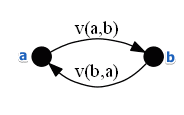
Voting Theory Analog

We can see the valued preference function as the proportion voters:

• $v(a, b)$ is the proportion of voters who prefer $a$ to $b$
• $v(b, a)$ is the proportion of voters who prefer $b$ to $a$, $v(b, a) = 1 - v(a, b)$

This is quite similar to Condorcet's Rule:

• $v(a, b) = \cfrac{N(a > b)}{N}$ and $v(b, a) = \cfrac{N(b > a)}{N}$

Sources

• Decision Engineering (ULB)