Modeling Preferences
To be able to find the best solution for MCDA problems we need to know ‘‘subjective preferences’’:
- these are binary relations provided by a decision maker
- defined analogously to Voting Theory Relations
So given two alternatives $a$ and $b$ a decision maker can say if
- $a \ P \ b$ or $b \ P \ a$: $a$ is preferred to $b$ - ‘‘the preference relation’’
- $a \ I \ b$ - the indifference relation
- $a \ J \ b$ - the incomparability relation, when you cannot compare things
Main properties:
- $P$ is asymmetric
- $a \ P \ b \equiv b \ \overline{P} \ a$
- $I$ is reflexive and symmetric:
- $a \ I \ a$ and $a \ I \ b \equiv b \ I \ a$
- $J$ is irreflexible and symmetric
- $a \ \overline{J} \ a$ and $a \ J \ b \equiv b \ J \ a$
Transitivity
- $P$ is transitive
- but $I$ is not| by Luce’s Coffee Cups (In contract to Voting Theory - there we assumed it’s transitive) | | We can show the preferences of a decision maker with a graph:
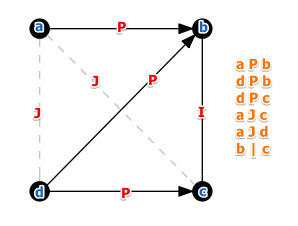
Preference Structures
How to build a mathematical model from statements of a decision maker?
There are several preference structures that can do that:
- Complete Pre-Order Preference Structure ($I$ is not transitive) - The Traditional Model
- SemiOrder Preference Structure ($I$ is transitive, no $J$) - The Threshold Model
- Partial Order Preference Structure (with $J$)
- Valued Preference
Preferential Independence
This is an important condition between preferences and criteria: the criteria should be preferentially independent.