Subspaces
A subspace of a Vector Space is a vector space on its own
Illustration by example
Suppose we have a space $\mathbb R^n$ (e.g. $\mathbb R^2$)
What if we removed one vector? Say, we remove $\bf 0$?
- The space becomes no longer closed under multiplication by scalar. $\forall \mathbf x: \mathbf 0 \cdot \mathbf x = 0$ which we removed.
- this is not a vector space - it must be closed under all operations
Another candidate:
- let’s consider the positive quarter of the $x/y$ plane (where $x_1, x_2 > 0$):

- let’s take a vector $\vec x$ from there and multiply it by -1. We no longer stay in this quarter.
- So this is not a vector space
Any line through the origin:

- is it a vector space?
- yes. We can take any scalar, and the result will still be on the line
- if the line is not through the origin, then multiplying by 0 will bring us out of the space - so the origin must be included
So, a ‘‘subspace’’ of a space should form a space on its own: it should be closed under all possible operations on elements in the subspace
Subspaces of $\mathbb R^2$
- whole $\mathbb R^2$
- any line through the origin $\mathbf 0_2$
- only vector $\mathbf 0_2$
Subspaces of $\mathbb R^3$
- whole $\mathbb R^3$
- only vector $\mathbf 0_3$
- any line through the origin $\mathbf 0_3$
- any plane through the origin $\mathbf 0_3$
Subspaces from Matrices
For a Matrix there are Four Fundamental Subspaces:
Column Space
Suppose we have a matrix $A \in \mathbb R^{3 \times 2}$
$A = \begin{bmatrix}
1 & 3
2 & 3
4 & 1
\end{bmatrix}$
Subspace from columns - $C(A)$ - the Column Space of $A$:
- we cannot just take the two columns and call it a subspace:
- it also must include all linear combinations of these columns
- these linear combinations of two vectors form a plane - a subspace $\mathbb R^2$ in the space $\mathbb R^3$
- since we include all possible combinations, we’re guaranteed to have a subspace
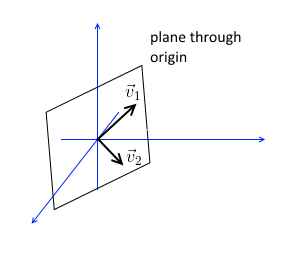
- $v_1$ and $v_2$ are 1st and 2nd columns of $A$ - they form a plane through the origin
Subspace Properties
Take $\mathbb R^3$ and 2 subspaces: $P$ (plane) and $L$ (line)
- is $P \cup L$ a subspace?
- $P \cup L$ $\equiv$ all vectors in $P$ or $L$ or both
- not a subspace: take $v_1 \in P$ and $v_2 \in L$. $v_1 + v_2$ maybe somewhere else - go outside of the union
- is $P \cap L$ a subspace?
- $P \cap L \equiv$ vectors in both $P$ and $L$
- yes (see reasoning below)
$S \cap T$ is a subspace:
- if $v, w \in S$ then $v + w \in S$ (and all linear combinations)
- if $v, w \in T$ then $v + w \in T$ (and all linear combinations)
- then if $v, w \in S \cap T$ then $v + w \in S \cap T$
Sources
- Linear Algebra MIT 18.06 (OCW)
- Курош А.Г. Курс Высшей Алгебры