ML Wiki

B-Tree

B+ Tree

A search tree is a way to organize data to allow efficient

  • B-Tree - same idea, but for secondary memory, for blocks
  • A B+ Tree variation of B-Tree. Here if B-Tree is mentioned, it's usually referred to B+ Tree

btree-ex.png

  • consists of leaf nodes and intermediate nodes


Order of Tree

parameter $n$ is the order of a tree

  • it determines the layout of the block
  • each block will have
    • $n$ search keys
    • $n + 1$ pointer

Example

  • suppose our block has size 4096 bytes
  • integers are 4 bytes long, pointers are 8 bytes long
  • suppose there's no header
  • then we want such $n$ that $4n + 8(n + 1) \leqslant 4096$
  • that $n = 340$

Example 2

  • block size 4096
  • 8 bytes per pointer and 8 bytes per key
  • $(n + 1) \cdot 8 + n \cdot 8 \leqslant 4096$
  • $n = 255$: we can store 256 pointers and 255 keys in one block


Height

How to estimate height?

  • Suppose $128 \times 10^6$ tuples in $R$
  • we have a b-tree index with order $n = 255$ on attribute $C$
  • assuming all leaf blocks are full, what's the height?
    • so there are $\left\lceil \cfrac{128 \times 10^6}{255} \right\rceil$ leaf blocks
    • $\left\lceil \cfrac{128 \times 10^6}{255^2} \right\rceil$ blocks at level 2
    • $\left\lceil \cfrac{128 \times 10^6}{255^3} \right\rceil$ blocks at level 3
    • ...
    • $\left\lceil \cfrac{128 \times 10^6}{255^h} \right\rceil$ blocks at level $h$
    • so it's logarithm
  • $h = \lceil \log_{255} (128 \cdot 10^6) \rceil = 4$
  • so #Lookup is 4 + 1 I/Os

What if blocks are half-full?

  • since leaves are half-full, they keep 128 records
  • $h = \lceil \log_{128} (128 \cdot 10^6) \rceil = 4$
  • again 4 + 1 I/Os


Non-Leaf Node

btree-leaf-ex.png

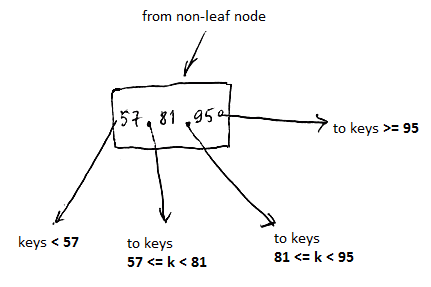
  • $n$ search keys, $n + 1$ pointers
  • first pointer points to keys that are strictly less than the first key
  • last pointer points to keys that are greater or equal to the last key
  • for in-between pointers, if $k_i$ is a key, and $p_{i-1}$ and $p_i$ are pointers around it, then $p_{i-1} \leqslant k_i < p_i$


Leaf Node

btree-non-leaf-ex.png

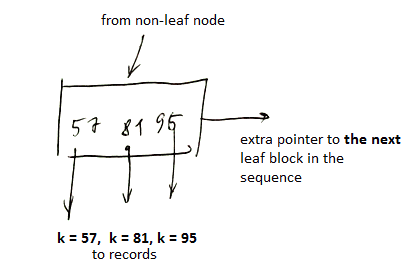
  • $n$ keys,
  • $n$ pointers to actual records, 1 extra pointer to the next leaf in the sequence


Balancing

Reasons

  • I/O cost of looking up is the longest path from the root to a leaf
  • so we want our tree be balanced:
  • to have paths as short as possible - with all the leaves at the same depth

Idea

  • Recall that for $n$ we have $n + 1$ pointers and $n$ keys
  • we don't want to have too empty nodes
  • so we will require all nodes to be at least half-full

Size Invariants

nodes are half-full:

  • at least $\left\lceil \cfrac{n + 1}{2} \right\rceil$ pointers for non leaf
  • at least $\left\lfloor \cfrac{n + 1}{2} \right\rfloor$ pointers for leaf
  • the only exception is root: it can contain any number of pointers

for example

  • btree-invariants-ex.png
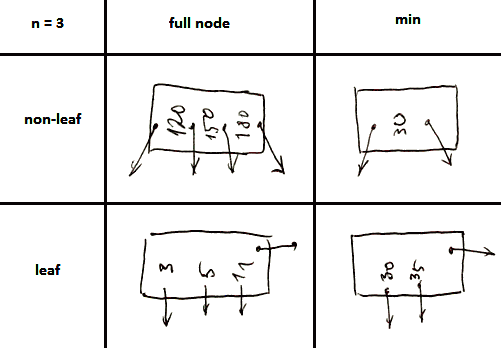
  • note that for leaf nodes a pointer to the next node counts as well
max # pointers max # keys max # pointers to data min # keys
non-leaf $n + 1$ $n$ $\left\lceil \cfrac{n + 1}{2} \right\rceil$ $\left\lceil \cfrac{n + 1}{2} \right\rceil - 1$
leaf $n + 1$ $n$ $\left\lfloor \cfrac{n + 1}{2} \right\rfloor$ $\left\lfloor \cfrac{n + 1}{2} \right\rfloor$
root $n + 1$ $n$ 2 1


Operations

Cost of operations are expressed in I/O Model of Computation

Lookup

suppose we are looking for $k = 35$

  • btree-ex.png

Algorithm

  • start at the root
  • follow the suitable pointer (as described in #Leaf Node) - this is the left root pointer
  • for the next, take the last ($k \geqslant 35$)
  • and finally read the block
  • btree-ex-lookup.png

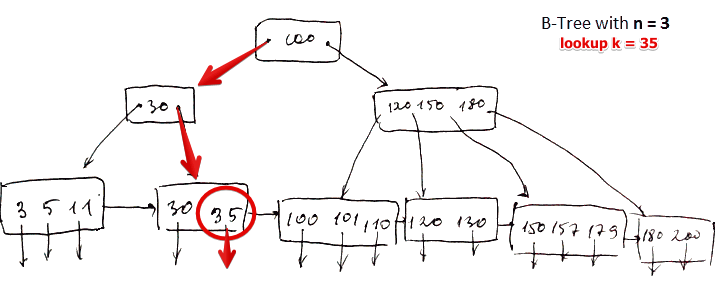
I/O Cost

  • head of the tree + 1 I/O to read
  • for $k = 35$: 3 I/O
  • for $k = 40$ (which doesn't exist): same path as for $k = 35$, cost is 3 I/O
  • so I/O cost = the longest path from the root to leaf (which is why we want it balanced)

Range Lookups

  • BTree supports range queries as well
  • such as $35 \leqslant k \leqslant 40$
  • we lookup the key corresponding to the left range boundary
  • since we have a pointer to the next block, we follow it until we hit the right range boundary
  • I/O cost in this case is
    • length of the path from the root to the leaf
    • then the number of leaves that we need to follow
    • and also we need to follow a pointer for each key in the range


Insert

4 cases

  • simple case - space available in leaf
  • leaf overflow
  • intermediate node overflow
  • new root

Simple Case

  • btree-insert-case1.png
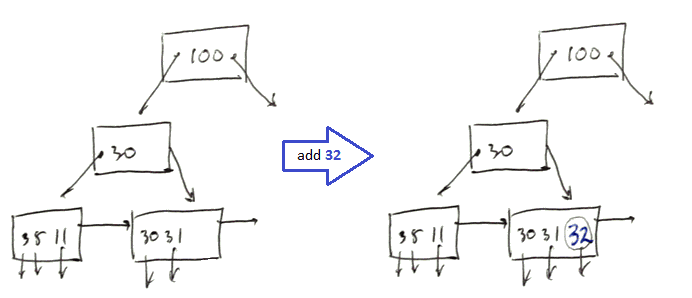
  • add $k = 32$
  • look up $k$ to identify the block where it should be stored
  • we have some room there - so just add the record there

Leaf Overflow

  • btree-insert-case2.png
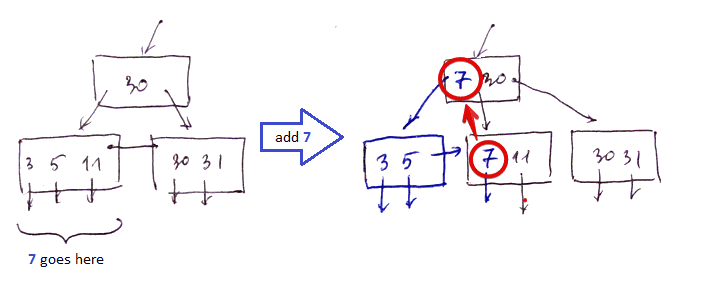
  • add $k = 7$
  • look up the block for 7, but it's fyll
  • so we split this block
    • create a new one and re-distribute items between them
    • this way they both become half-full (the invariant is maintained)
  • then in the new block we have some space (Simple Case) and we can put this record there

Intermediate Node Overflow

  • btree-insert-case3.png
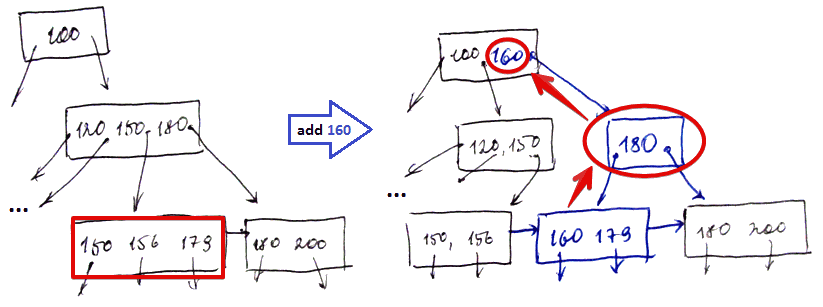
  • add $k = 160$ ($n = 3$)
  • there's no room in $\fbox{150, 156, 179}$ to add $160$ (Leaf Overflow case)
    • so we create a new block and re-distribute the keys between them
  • since we created a new block, we need to add a pointer to it, but there is no room in $\fbox{120, 150, 180}$
  • so we split the intermediate block and move $180$ to the new block
  • also need to modify the root block to add pointer to the new block $\fbox{180}$

New Root

  • sometimes we need to create a new root
  • btree-insert-case4.png
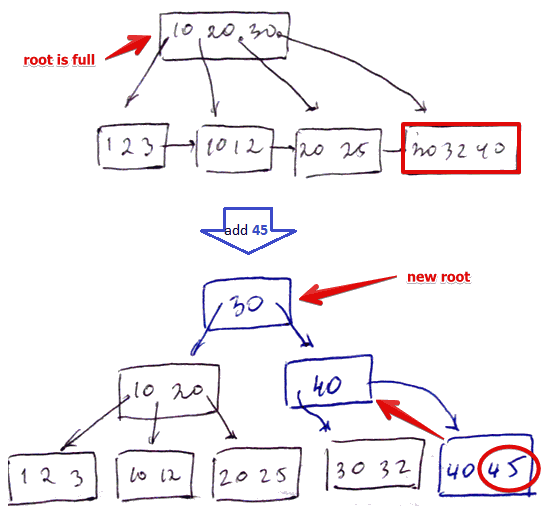
  • add $k = 45$ ($n = 3$)
  • we cannot add it to $\fbox{30, 32, 40}$ (Leaf Overflow case)
    • split it to 2 nodes, need to add the pointer to the new node
  • cannot add it to $\fbox{10, 20, 30}$ (Intermediate Node Overflow case)
    • split it into 2 nodes, need to add the pointer to new block
  • but $\fbox{10, 20, 30}$ is a root!
    • need to split it to two nodes
    • and promote $\fbox{30}$ to the root


I/O Cost

  • operations
    • search
    • create a new block (split, write two blocks): 2 operations
    • go level up
  • so in the worst case 2 I/O at each level + possibly writing a new root (1 I/O)
  • then the total cost is
    • $\text{depth} + 2 \times \text{depth} + 1 = 3 \times \text{depth} + 1$


Deleting

Again 4 cases

  • Simple - just delete it
  • Coalesce Leaf With Siblings
  • Redistribute Keys
  • Intermediate Nodes Coalescing

Coalesce Leaf With Siblings

  • btree-delete-case2.png
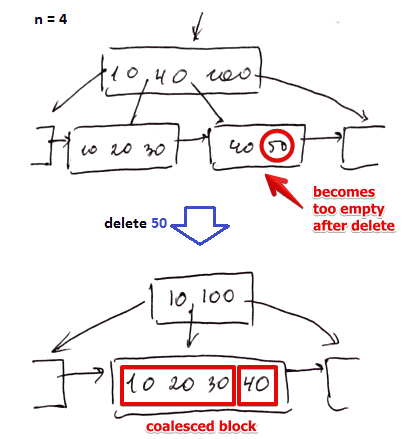
  • we delete $k = 50$ ($n = 4$)
  • we locate the block with 50 and remove this record from it
  • now the block becomes too empty (recall #Size Invariants)
  • so we coalesce it with $\fbox{10, 20, 30}$
  • now we have a new block, and the old one is not needed anymore - we remove it
  • additional bookkeeping: need to make sure the next pointer point to the record the old block pointed to

Redistribute Keys

  • btree-delete-case3.png
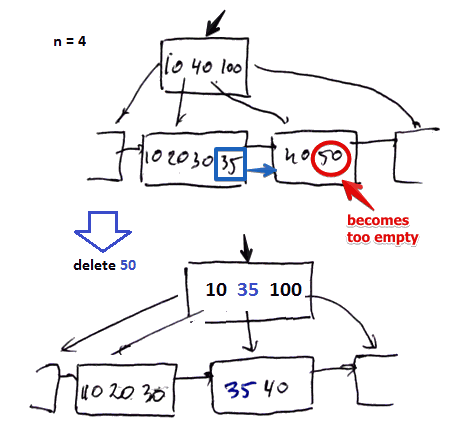
  • we delete $k = 50$ ($n = 4$)
  • when we delete 50, the block that contained it becomes almost empty
  • cannot coalesce with $\fbox{10, 20, 30, 35}$ because it's full
  • so to fix that we borrow a key from $\fbox{10, 20, 30, 35}$ to become half-full again
  • and update the parents accordingly

Intermediate Nodes Coalescing

  • btree-delete-case4.png
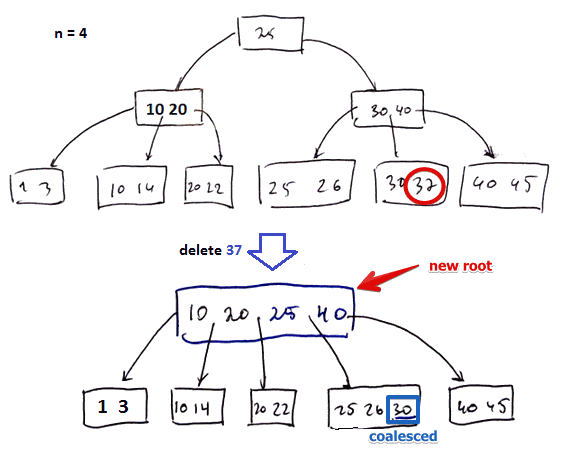
  • we delete $k = 37$ ($n = 4$)
  • first we locate the block with 37 and remove the record from it (Coalesce Leaf With Sibling case)
    • since this block $\fbox{30}$ becomes too small we coalesce it with $\fbox{25, 26}$
    • need to remove the pointer to the deleted block from the parental node $\fbox{30, 40}$
    • i.e. we remove 30 from there
  • but then the parental also node becomes too small, so we coalesce it with its sibling as well
  • finally we don't need the root $\fbox{25}$ anymore since new block $\fbox{10, 20, 25, 40}$ can reference all the records

I/O Cost

Cost

  • search: depth of the tree
  • remove and regroup: 2 I/Os at each level
  • no need to follow the pointer (i.e. don't do +1 as with #Insertion)
  • total: $\text{depth} + 2 \times \text{depth} = 3 \times \text{depth}$


Multiple Keys

Sometimes we want to address a key made of several keys

Lexicographical Order

For B-Trees have to be ordered somehow

  • we may need to compare tuples in lexicographical order
    • so we define this ordering as
    • $(x, y, z) \leqslant (x', y', z') \iff \\ x < x' \lor (x = x' \land y < y') \lor (x = x' \land y = y' \land z \leqslant z')$

Problem with Lexicographical Order

Assume index of (age, salary) pairs with lexicographical order

  • btree-lex-ord.png
  • query age < 20 - ok
    • start at the beginning of index ans scan till see 20
  • query salary < 30 - not fine
    • linear scan, need to scan everything
  • query age < 20 $\land$ sal < 20
    • also scan index till see 20,
    • meanwhile filtering records with sal < 20
  • so using lexicographical ordering doesn't allow all queries we want

need other types of indexes - Multi-Dimensional Indexes

  • R-Tree in particular: it's generalization of B-Trees to multidimensional data


See also


Sources

Retrieved from "http://mlwiki.org/index.php?title=B-Tree&oldid=182"