ML Wiki

R-Tree

This is Tree-Based Multi-Dimensional Index Structure

• Generalization of a B-Tree to multidimensional space
• Indexes regions

B-Tree

In a B-Tree we can view a node as a line (1-dimensional space)

• 
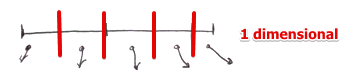
• and it divides a line into segments

R-Tree

Same, but for 2D and more

• we divide data into data regions
• interior nodes of an R-Tree correspond to interior region
  • not data region as in B-Tree, but just a region
• A region can be of any shape, but usually it's a rectangle or other simple shape
• A node has subregions - its children
  • subregions are allowed to overlap
  • but it's usually better to keep the overlap small

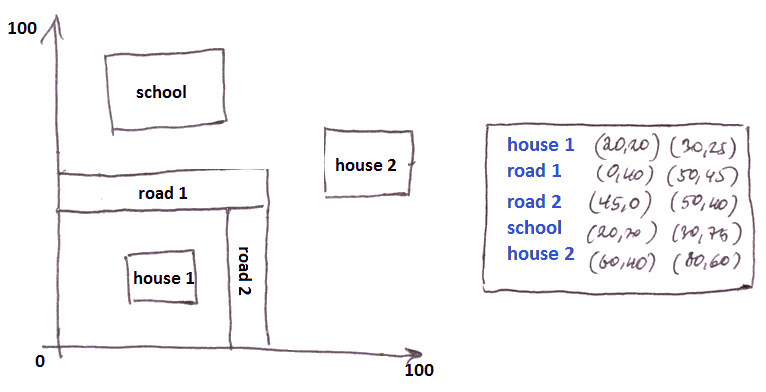
Example

Suppose we have a region

• it fits in one block
  • 
• but we insert an new object - and it no longer fits
  • need to split the block into two regions
  • 
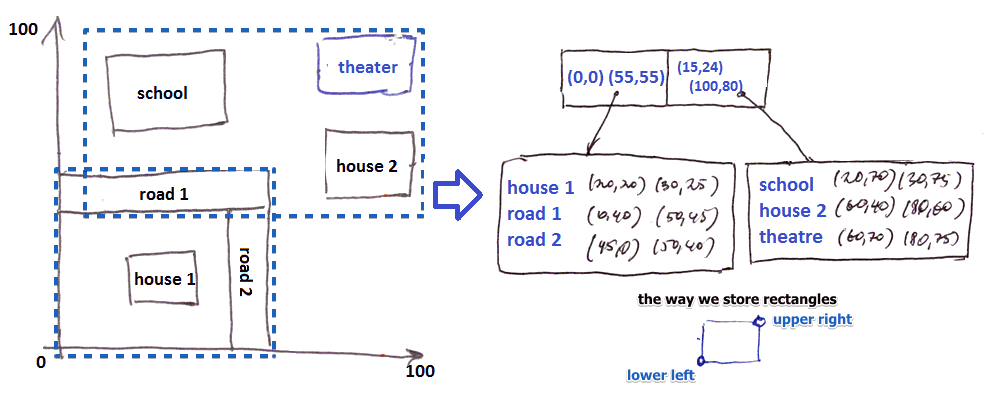
  • note that (a) the blocks overlap and (b) how we represent these blocks in out database
• when we insert next time, a new object can be added to an existent block
  • 
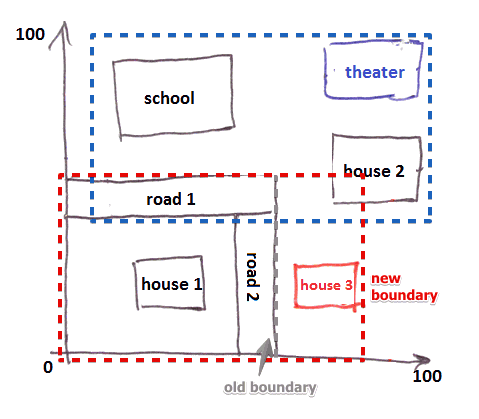
  • note that we have to adjust regions boundaries to include the new object

Operations

Lookup

specify a point $P$ and ask what regions $P$ lies in (where-am-I query)

• start with the root
• find which children correspond to interior regions that contain $P$
• if there are no such regions - we're done ($P$ doesn't belong to any region)
• if there are more than 1 region - apply recursively to each
• when we reach the leaf regions - we find the actual data regions

Insert

• start at root and try to find a region where $R$ fits
• if found: go inside and repeat
• if not: need to expand an existing region
  • we want to expand as little as possible
  • so we find the one that gives the smallest expansion
• when we reach a leaf, we insert $R$
• if there's no room - we split it
  • remember that we want regions to be as small as possible
  • so we find the split that gives us that
  • after that we insert the new subregion to the leaf's parent
  • essentially the same procedure as for B-Tree

Summary

Good for:

• Where-am-I (point) queries
• Finding intersecting regions (e.g. when a user selects an area on map)
• Partial Range queries
• Range queries
• nearest neighbor

Also

• Always balanced
• often used in practice

See also

• B-Tree and Binary Search Trees
• Multi-Dimensional Indexes
• kd-Trees and Quad Trees
• Spatial Databases

Sources

• Database Systems Architecture (ULB)
• Database Systems: The Complete Book (2nd edition) by H. Garcia-Molina, J. D. Ullman, and J. Widom