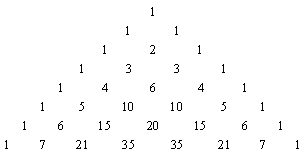Combinations

Combinations

Не всегда нас интересует порядок, в котором располагаются элементы - а интересует лишь состав.

Combinationsми размера $k$ из $n$ элементов называют всевозможные расстановки длины $k$, составленных из этих элементов и отличающихся лишь составом, а не порядком элементов.

$C_n^k$ - число сочетаний размера $k$, которые можно составить из $n$ элементов.

$P(n, n-k) = \frac{n| }{k! \cdot (n - k)!} = C_n^k$ | |Расставим по порядку все $n$ элементов и зашифруем каждое сочетание расстановкой размера $n$, состоящей из нулей и единиц. Если элемент входит, запишем 1, иначе 0. При этом каждому сочетанию будет соответствовать расстановка из $k$ единиц и $(n - k)$ нулей.

Задача

Сколькими способами можно поставить 8 ладей на поле 8 $\times$ 8? (Так, что они могут бить друг друга, а могут и не бить.)

• Нам нужно выбрать из 64 клеток любые 8.
• Следовательно, $C_{64}^8 = \frac{64| }{8! \cdot 56!}$ | |

  Combinations с повторениями

  Имеется $n$ различных типов предметов. Сколько комбинаций размера $k$ можно сделать из них, если не принимать во внимание порядок элементов в комбинациях?

=== Мотивирующий пример === В кондитерском магазине продают 4 типа пирожных: наполеон, эклеры, песочные и слоёные. Сколькими типами можно купить 7 пирожных?

Способ 1

• Зашифруем каждую покупку с помощью единиц и нулей.
• Сначала запишем сколько было куплено наполеонов, затем ноль, затем количество эклеров, ноль, песочных, ноль, и, наконец, слоёных.
• Получим $\underbrace{111} 0 \underbrace{1} 0 \underbrace{11} 0 \underbrace{1}$
• Разным покупкам при этом соответствуют различные перестановки с повторениями

$P(7, 3) = \frac{10| }{7! \cdot 3!} = 120$ | |#### Способ 2

• Расположим в каждой покупке пирожные по порядку (наполеоны, эклеры, песочные, слоёные)
• Затем пронумеруем их, при этом к номерам наполеонов прибавляя 0, к номерам эклеров 1, песочных 2, слоёных - 3.
• Самый большой номер - 7 + 3 = 10 для слоёного пирожного
• Самый маленький номер - 1 + 0 = 1 для наполеона
• Ни один номер при этом не будет повторятся и каждой возрастающей последовательности из 7 чисел будет соответствовать некоторая покупка

Например, имеем последовательность (2, 3, 4, 5, 7, 8, 9). Отнимем (1, 2, 3, 4, 5, 6, 7) и получим (1, 1, 1, 1, 2, 2, 2). Т.е. имеем 4 эклера (к эклерам мы прибавляли 1) и 3 песочных (к их номерам прибавляли 2).

• Таким образом, число способов купить 7 пирожных равно числу способов выбрать 7 предметов из 10:
• Ответ $C_{10}^7 = 120$

В общем случае задачи на сочетания с повторениями решаются так же.

Зашифруем каждую комбинацию нулями и единицами

• для каждого типа единицами запишем сколько предметов входит в комбинацию
• и разделим типы предметов между собой нулями

При этом получится столько единиц, сколько предметов нам нужно выбрать, т.е. $k$, и $(n - 1)$ нулей

• $\bar{C_n^k} = P(k, n - 1) = \frac{(k + n - 1)

  }{k! \cdot (n - 1)!}$

  - Следовательно, $\bar{C}n^k} = C{n + k - 1}^k$.

Аналогично можно прийти к этой формуле и вторым способом.

Разновидность

Встречаются задачи, в которые обязательно нужно включить элементы $r$ фиксированных типов, $r \leqslant n$

Для этого

• возьмем $r$ элементов нужного типа
• оставшиеся $k - r$ мест заполним остальными элементами, принадлежащими всем $n$ типам.

Итого, имеем формулу $\bar{C}n^{k - r}} = C{n + k - r - 1}^{k - r}$

Свойства сочетаний

Свойство 1

$C_n^k = C_n^{n - k}$

• Очевидно из формулы $C_n^k = \frac{n| }{(n - k)! \cdot k!}$ |- Если в формуле заменить $k$ на $(n - k)$, то $n - k$ заменится на $n - (n - k) = k$ - и множители просто поменяются местами |

  Свойство 2

  $C_n^k = C_{n - 1}^{k - 1} + C^k_{n - 1}$

• Составим все сочетания размера $k$ из $n$ элементов $a_1, a_2, …, a_n$ и разобъем на две группы:
  • в первых будут элементы, содержащие $a_n$
  • во второй не будет элементов, содержащих $a_n$
• если в первой группе откинуть $a_n$ (т.к. оно есть везде, то на количество сочетаний это не повлияет), то получится сочетания размера $k - 1$, составленные из элементов $a_1, a_2, …, a_{n - 1}$ (всего $n - 1$ элементов) .
  • Число сочетаний в первой группе равно $C_{n - 1}^{k - 1}$
• сочетания второй группы являются сочетаниями размера $k$, составленные из $n - 1$ элементов $a_1, a_2, …, a_{n - 1}$
  • Число сочетаний во второй группе равно $C_{n - 1}^k$
• По правилу суммы, общее число сочетаний равняется $C_{n - 1}^k + C_{n - 1}^{k - 1} = C_n^k$

Свойство 3

$\sum_{k = 0}^n C_n^k = 2^n$

• $2^n$ - число всех размещений с повторениями из элементов ‘‘двух типов’’.
• Разобьём эти размещения на $k$ групп
• в $k$-ю группу отнесем те элементы, в которые входят $k$ элементов первого типа и ($n - k$) элементов второго типа
• размещения, входящие в $k$-ю группу - всевозможные перестановки из $k$ элементов первого типа и $n - k$ второго
• число таких перестановок равно $P(k, n - k)$, а $P(k, n - k) = C_n^k$

В общем виде эту формулу можно записать так:

$\sum_{n_1 + … + n_k = n} P(n_1, …, n_k) = k^n$

(свойства 4 и 5 опущены - см. Виленкина)

=== Свойство 6 === $C_n^0 - C_n^1 + … + (-1)^n C_n^k = 0$

• $C_n^0 = C_{n - 1}^0 = 1$
• т.к. $C_n^1 = C_{n - 1}^0 + C_{n - 1}^1$, то $C_{n - 1}^0 - C_n^{1} = -C_{n - 1}^2$
• далее, имеем $-C_{n - 1}^2 + C_n^2 = C_{n - 1}^2$
• В конце концов все слагаемые взаимоуничтожаются

Некоторые свойства (особенно 3 и 6) очень легко доказываются с помощью бинома Ньютона

Треугольник Паскаля

Биномиальные коэффициенты можно вычислять с помощью свойства 2: $C_n^k = C_{n - 1}^{k - 1} + C^k_{n - 1}$. Если расположить $C_n^k$ по середине под $C_{n - 1}^{k - 1}$ и $C^k_{n - 1}$, то числа выстроятся в треугольник

Задача

<img src=”” />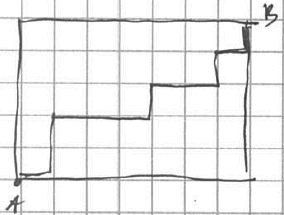

Сколькими способами можно добраться из вершины $A$ в вершину $B$, если двигаться можно только “вправо” и “вверх”?

<img src=”” />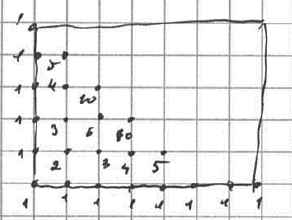

• Если записать число способов, которыми можно попасть в определенный узел, то мы увидим треугольник Паскаля.
• Действительно, в $k$-й узел $n$-й строки можно попасть либо из $(k-1)$-того, либо из $k$-го узла
• Поэтому число путей, ведущих в этот узел есть $C_n^k = C_{n - 1}^{k - 1} + C^k_{n - 1}$

Таким образом мы можем сформулировать одно из свойств треугольника Паскаля: Каждое число в треугольнике равно количеству способов добраться до него из вершины, перемещаясь либо вправо-вниз, либо влево-вниз.

See also

• Permutations
• Binomial Theorem

Sources

• Виленкин Н.Я. Комбинаторика. М., Наука, 1969.
• Генкин С.А., Итенберг И.В., Фомин Д.В. Ленинградские математические кружки, 1994.