Cosine Similarity

distances similarity-functions

Cosine Similarity

Cosine similarity is a Similarity Function that is often used in Information Retrieval

it measures the angle between two vectors, and in case of IR - the angle between two documents

Derivation

recall the definition of the Dot Product: $\mathbf v \cdot \mathbf w = | \mathbf v | \cdot | \mathbf w | \cdot \cos \theta$

- or, by rearranging get $\cos \theta = \cfrac{\mathbf v \cdot \mathbf w}{| \mathbf v | \cdot | \mathbf w - so, let’s define the cosine similarity function as $\text{cosine}(\mathbf d_1, \mathbf d_2) = \cfrac{\mathbf d_1^T \mathbf d_2}{| \mathbf d_1 | \cdot | \mathbf d_2 - cosine is usually $[-1, 1]$, but document vectors (see Vector Space Model) are usually non-negative, so the angle between two documents can never be greater than 90 degrees, and for document vectors $\text{cosine}(\mathbf d_1, \mathbf d_2) \in [0, 1]$

- min cosine is 0 (max angle: the documents are orthogonal)

max cosine is 1 (min angle: the documents are the same)

Cosine Normalization

If documents have unit length, then cosine similarity is the same as Dot Product

$\text{cosine}(\mathbf d_1, \mathbf d_2) = \cfrac{\mathbf d_1^T \mathbf d_2}{| \mathbf d_1 | \cdot | \mathbf d_2 - thus we can “unit-normalize” document vectors $\mathbf d’ = \cfrac{\mathbf d}{| \mathbf d - this “unit-length normalization” is often called “cosine normalization” in IR

== Cosine Distance ==

for documents $\text{cosine}(\mathbf d_1, \mathbf d_2) \in [0, 1]$
it is max when two documents are the same
how to define a distance? distance function should become larger as elements become less similar
since maximal value of cosine is 1, we can define ‘'’cosine distance’’’ as
$d_c(\mathbf d_1, \mathbf d_2) = 1 - \text{cosine}(\mathbf d_1, \mathbf d_2) = 1 - \cfrac{\mathbf d_1^T \mathbf d_2}{| \mathbf d_1 | \cdot | \mathbf d_2 \ |
Metricity

Let’s check if cosine distance is a proper metric, i.e. it satisfies all the requirements
Let $D$ be the document space and $\mathbf d_1, \mathbf d_2 \in D$
$d_c(\mathbf d_1, \mathbf d_2) \geqslant 0$: checks - 0 is minimum
$d_c(\mathbf d_1, \mathbf d_1) = 0$ checks - $1 - \cos 0 = 0$
$d_c(\mathbf d_1, \mathbf d_2) = d_c(\mathbf d_2, \mathbf d_1)$: checks - angle is the same

What about the triangle inequality?

under certain conditions is doesn’t hold (Korenius2007) - so it’s not a proper metric

Cosine and Euclidean Distance

Euclidean distance $| \mathbf d_1 - \mathbf d_2 | = \sqrt{(\mathbf d_1 - \mathbf d_2)^T (\mathbf d_1 - \mathbf d_2)}$ |- ED is a proper metric

There’s a connection between Cosine Distance end Euclidean Distance

consider two unit-normalized vectors $\mathbf x_1 = \mathbf d_1 / | \mathbf d_1 |$ and $\mathbf x_2 = \mathbf d_1 / | \mathbf d_1 |$

- if vectors are unit-normalized, cosine = dot product, so we have

$| \mathbf x_1 - \mathbf x_2 |^2 = 2 \, (1 - \mathbf x_1^T \mathbf x_2) = 2 \, \big(1 - \text{cosine}(x_1, x_2)\big) = 2 \, d_c(x_1, x_2)$

It can also make some sense visually:

recall the Cosine Theorem: $a^2 = b^2 + c^2 - 2 bc \cos \theta$
$b = c = 1$, so we have $a^2 = 2 \, (1 - \cos \theta)$

Thus we can use Euclidean distance and interpret it as Cosine distance

Other Properties

Translation Non-Invariant

For PCA we usually do mean-correction

but mean-correction affects the angle between documents
can show that visually: the angle between two vectors are not translation-resistant
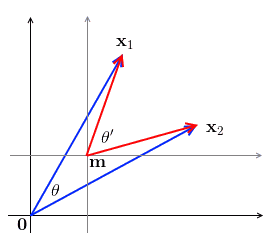
i.e. if we have two vectors $\mathbf x_1$ and $\mathbf x_2$ and with $\theta$ being the angle between them, when we translate the space by $m$, we get a new angle $\theta’$ s.t. $\theta \ne \theta’$
also note that when we translate, some elements may become negative

Sources

Korenius, Tuomo, Jorma Laurikkala, and Martti Juhola. “On principal component analysis, cosine and Euclidean measures in information retrieval.” 2007. [http://www.sciencedirect.com/science/article/pii/S0020025507002630]

✏️ Edit on GitHub

Cosine Similarity