ML Wiki

Cumulative Gain Chart

Cumulative Gain Chart

Gain Charts are used for Evaluation of Binary Classifiers

  • also it can be used for comparing two or more binary classifiers
  • the chart shows $\text{tpr}$ vs $\text{sup}$


Motivating Example

Suppose we have a direct marketing campaign

  • population is very big
  • we want to select only a fraction of the population for marketing - those that are likely to respond
  • we build a model that scores receivers - assigns probability that he will reply
  • want to evaluate the performance of this model


Cumulative Gain

Performance evaluation

  • recall values that can be calculated for Evaluation of Binary Classifiers
  • accuracy - but it's not enough here
  • $\text{tpr}$ - True Positive Rate or Sensitivity
    • $\text{tpr} = \cfrac{\text{TP}}{\text{TP} + \text{FN}}$
    • fraction of examples correctly classified
  • $\text{sup}$ - Support (Predictive Positive Rate)
    • $\text{sup} = \cfrac{\text{TP} + \text{FP}}{N} = \cfrac{\text{predicted pos}}{\text{total}}$
    • fraction of positively predicted examples

Suppose that we obtained the following data:

  • Cls = actual class
  • score = predicted score


Cls Score
N 0.01
P 0.51
N 0.49
P 0.55
P 0.42
N 0.7
P 0.23
N 0.39
P 0.04
N 0.19
P 0.12
N 0.15
N 0.43
P 0.33
N 0.22
N 0.11
N 0.31
P 0.8
P 0.9
P 0.6
$\Rightarrow$ sort $\Rightarrow$
# Cls Score
1 P 0.9
2 P 0.8
3 N 0.7
4 P 0.6
5 P 0.55
6 P 0.51
7 N 0.49
8 N 0.43
9 P 0.42
10 N 0.39
11 P 0.33
12 N 0.31
13 P 0.23
14 N 0.22
15 N 0.19
16 N 0.15
17 P 0.12
18 N 0.11
19 P 0.04
20 N 0.01
  • sort the table by score desc
  • max on top, min at bottom
  • if model works well, expect
    • responders at top
    • non-responders at bottom
  • the better the model
    • the clearer the separation
    • between positive and negative


Intuition

  • suppose now we select top 20% records
  • we see that out of 4 examples 3 of them are positive
  • in total, there are 10 responders (positive classes)
  • so with only 20% (4 records) we can target 3/10 = 30% responders
  • we also can use a random model
    • if you randomly sample 20% of records, you can expect to target only 20% your responders
    • 20% of 10 = 2
  • so we're doing better than random
  • can do it for all possible fractions of our data set and get this chart:


e7967fd0250d439d86771ec15aa3dd28.gif


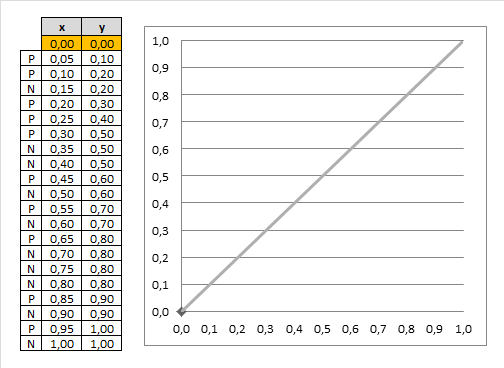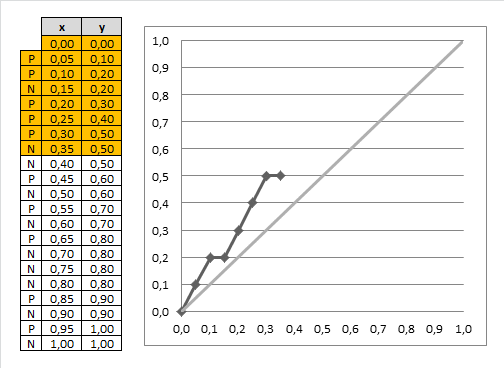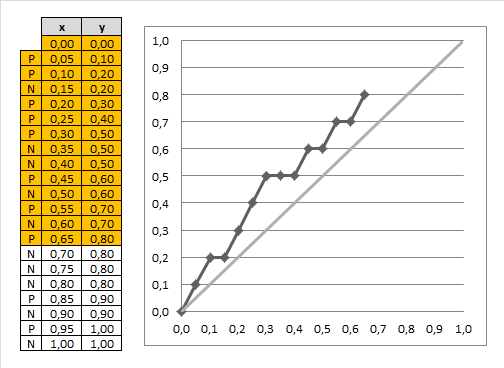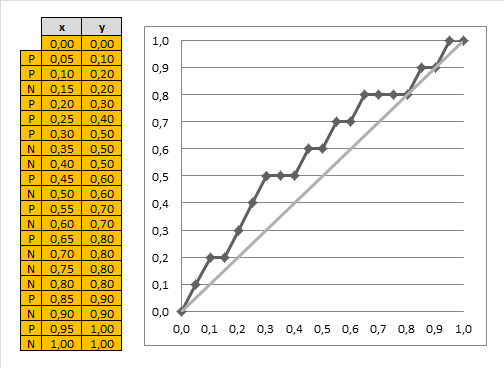
Best classifier

  • the optimal classifier will score positives and negatives s.t. there's a clear separation between them
  • in such a case the gain chart will always go up until it reaches 1, and then go left
  • gain-chart-ex.png
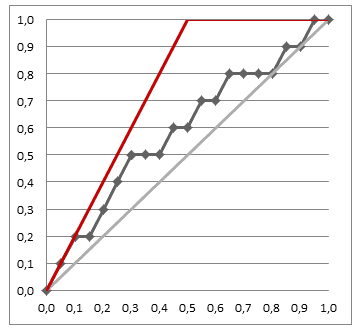
  • the closer our chart to the best one, the better our classifier is


Gain Chart

So a gain chart shows

  • Predicted Positive Rate (or support of the classifier)
  • vs True Positive Rate (or sensitivity of the classifier)
  • gain-chart.png
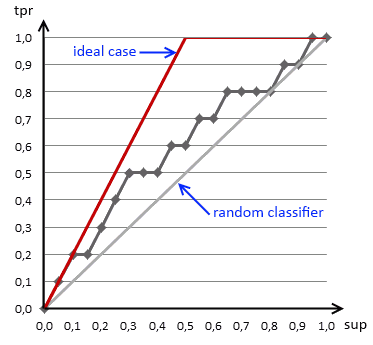
  • it says how much population we should sample to get the desired sensitivity of our classifier
  • i.e. if we want to direct 40% of potential repliers to our targeting campaign, we should select 20%


Cross-Validation

  • when we divide our data into two subsets, we can plot the charts for both
  • gain-chart-ex2.png
  • we can easily see if a classifier overfits on the test set, but underperforms on the testing


Examples

Given

  • 20 training examples, 12 negative and 8 positive
# Cls Score
1 N 0.18
2 N 0.24
3 N 0.32
4 N 0.33
5 N 0.4
6 N 0.53
7 N 0.58
8 N 0.59
9 N 0.6
10 N 0.7
11 N 0.75
12 N 0.85
13 P 0.52
14 P 0.72
15 P 0.73
16 P 0.79
17 P 0.82
18 P 0.88
19 P 0.9
20 P 0.92
$\Rightarrow$ sort(score)
# Cls Score
20 P 0.92
19 P 0.9
18 P 0.88
12 N 0.85
17 P 0.82
16 P 0.79
11 N 0.75
15 P 0.73
14 P 0.72
10 N 0.7
9 N 0.6
8 N 0.59
7 N 0.58
6 N 0.53
13 P 0.52
5 N 0.4
4 N 0.33
3 N 0.32
2 N 0.24
1 N 0.18

gain-chart-ex5.png


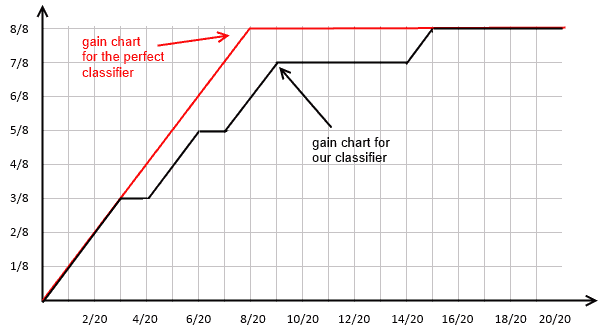
Comparing Binary Classifiers

Can draw two or more gain charts over the same plot

  • and thus be able to compare two or more classifiers
  • gain-chart-ex3.png
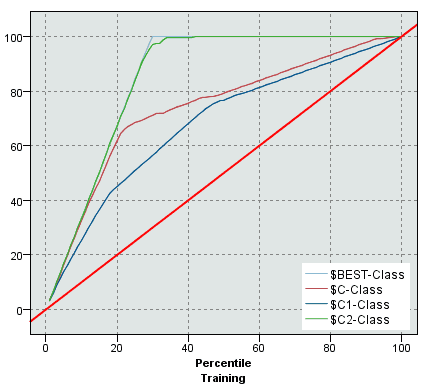
  • we see that one of the classifiers most likely overfits the training data
  • gain-chart-ex4.png
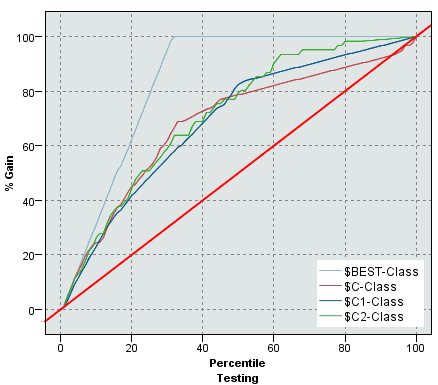
  • but when we test, we see that it performs as good (bas) as other classfiers


Plotting Gain Chart in R

In R there's a package called ROCR [1] (for drawing ROC Curves) 

install.packages('ROCR')
require('ROCR')

It can be used for drawing gain charts as well: 

cls = c('P', 'P', 'N', 'P', 'P', 'P', 'N', 'N', 'P', 'N', 'P', 
        'N', 'P', 'N', 'N', 'N', 'P', 'N', 'P', 'N')
score = c(0.9, 0.8, 0.7, 0.6, 0.55, 0.51, 0.49, 0.43, 
          0.42, 0.39, 0.33, 0.31, 0.23, 0.22, 0.19, 
          0.15, 0.12, 0.11, 0.04, 0.01)

pred = prediction(score, cls)
gain = performance(pred, "tpr", "rpp")

plot(gain, col="orange", lwd=2)

gain-r1.png

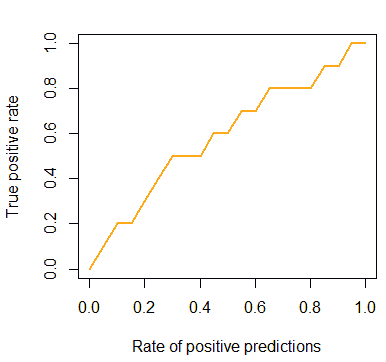
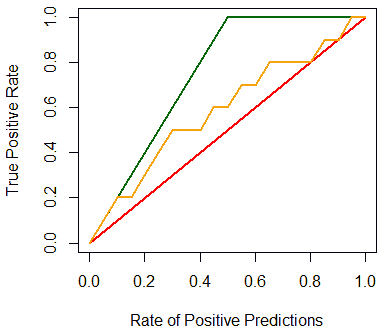
But we also can add the baseline and the ideal line: 

plot(x=c(0, 1), y=c(0, 1), type="l", col="red", lwd=2,
     ylab="True Positive Rate", 
     xlab="Rate of Positive Predictions")
lines(x=c(0, 0.5, 1), y=c(0, 1, 1), col="darkgreen", lwd=2)

gain.x = unlist(slot(gain, 'x.values'))
gain.y = unlist(slot(gain, 'y.values'))

lines(x=gain.x, y=gain.y, col="orange", lwd=2)

gain-r2.png


Cumulative Lift Chart

Lift charts show basically the same information as Gain charts

  • $\text{ppr}$ Predicted Positive Rate (or support of the classifier)
  • vs $\cfrac{\text{tpr}}{\text{ppr}}$ True Positive over Predicted Positive
  • lift-chart-ex.png


See Also

Sources

Retrieved from "http://mlwiki.org/index.php?title=Cumulative_Gain_Chart&oldid=472"