Cross-Validation
Contents
Test Errors
How you can tell that a hypothesis overfits?
- plotting - not always good
We can split all the data into 2 subsets
- training set $\approx$ 70% of data, $m$ - number of examples in the training set
- testing set $\approx$ 30% of data, $m_{\text{test}}$ - number of examples in the testing set
it's better to choose examples for training/testing sets randomly
| Prediction | Classification | |
|---|---|---|
| Example Model | Linear Regression | Logistic Regression |
| Test Error | $J_{\text{test}}(\theta) = \cfrac{1}{m_{\text{test}}} \sum \text{error} \big(h_{\theta}(x_{\text{test}}^{(i)}), y_{\text{test}}^{(i)} \big)$ | |
| $\text{error}(h_{\theta}(x), y)$ | Average Square Error $\text{error}(h_{\theta}(x), y) = \cfrac{1}{2} (h_{\theta}(x) - y)^2$ |
Misclassification Error $\text{error}(h_{\theta}(x), y) = \left\{\begin{array}{l} 0 \text { if classification is correct} \\ 1 \text{ otherwise} \end{array}\right.$ |
Cross-Validation
Generally cross-validation is used to find the best value of some parameter
- we still have training and test sets
- but additionally we have a cross-validation set to test the performance of our model depending on the parameter
Motivation: Model Selection Problem
We have a following problem of Model Selection
- Suppose we are about to create a model and not sure what degree of polynomial to choose
So the problem
- So we want to try 10 models
- let $d$ denote the degree of polynomial
- $d=1: h_{\theta} = \theta_0 + \theta_1 x$
- $d=2: h_{\theta} = \theta_0 + \theta_1 x + \theta_2 x^2$
- ...
- $d=10: h_{\theta} = \theta_0 + \theta_1 x + \theta_2 x^2 + ... + \theta_{10} x^{10}$
Results
- Each $d$ will give us a vector (or matrix) $\theta^{(d)}$
- Now we can try all $d$ models and see which gives the best (lowest) $J_{\text{test}}(\theta^{(i)})$
- Let's say we decided to choose 5th model
How well this model generalize?
- the test error is $J_{\text{test}}(\theta^{(5)})$
- but $J_{\text{test}}(\theta^{(5)})$ is a very optimistic estimate of the generalization error
- (because the lowest/best error was picked up - so the test error might be biased towards that)
- i.e. we the extra parameter $d$ was fit to test, and it's not fair to estimate our hypothesis on the test set, because we already used that set to get the best $d$
To address that problem
- instead of splitting the data set into 2 categories, we split into 3 sets:
- training set ($\approx$ 60%)
- $x^{(i)}, y^{(i)}$, total $m$ examples
- cross-validation set (or cv, $\approx$ 20%)
- $x_{\text{cv}}^{(i)}, y_{\text{cv}}^{(i)}$, total $m_{\text{cv}}$ examples
- test set ($\approx$ 20%)
- $x_{\text{test}}^{(i)}, y_{\text{test}}^{(i)}$, total $m_{\text{test}}$ examples
Now we can define
- Training error
- $J(\theta) = J_{\text{train}}(\theta) = \cfrac{1}{2m} \sum \text{cost}(x^{(i)}, y^{(i)})$
- Cross-Validation error
- $J_{\text{cv}}(\theta) = \cfrac{1}{2m_{\text{cv}}} \sum \text{cost}(x_{\text{cv}}^{(i)}, y_{\text{cv}}^{(i)})$
- Test Error
- $J_{\text{test}}(\theta) = \cfrac{1}{2m_{\text{test}}} \sum \text{cost}(x_{\text{test}}^{(i)}, y_{\text{test}}^{(i)})$
So for Model Selection to fit $d$, we
- obtain $\theta^{(1)}, ..., \theta^{(d)}$ and select best (lowest) $J_{\text{cv}}(\theta^{(i)})$
- estimate generalization error for the test set $J_{\text{test}}(\theta^{(i)})$
Tuning Learning Parameter
General algorithm
- Split data set into
- Learning set
- Validation set
- Test set
- use validation set for tuning control parameters
- use test set only for final evaluation
Let $\gamma$ be the control parameter
- for every possible value of $\gamma$
- build a classification model $C$ using the learning set
- use the validation set to estimate the expected error rate of $C$
- select the optimal value of the control parameter
- that is the value of $\gamma$ s.t. the error rate is minimal
Regularization Parameter $\lambda$
Suppose now we're fitting a model with high-order polynomial
- $h_{\theta}(x) = \theta_0 + \theta_1 x + ... + \theta_4 x^4$
- to prevent overfitting we use regularization
- $J(\theta) = \cfrac{1}{m} \sum \text{cost}(h_{\theta}(x^{(i)}), y^{(i)}) + \cfrac{\lambda}{2m} \sum_{j=1}^{m} \theta_j^2$
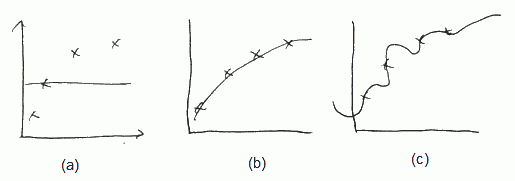
- (a) If $\lambda$ if large (say $\lambda = 10000$), all $\theta$ are penalized and $\theta_1 \approx \theta_2 \approx ... \approx 0$, $h_{\theta}(x) \approx \theta_0$
- (b) if $\lambda$ is intermediate, we fit well
- (c) if $\lambda$ is small (close to 0) we fit too well, i.e. we overfit
How can we chose good $\lambda$? Let's define
- $J_{\text{train}}(\theta) = \cfrac{1}{m} \sum \text{cost}(h_{\theta}(x^{(i)}), y^{(i)})$ (same as $J(\theta)$, but without regularization)
- $J_{\text{cv}}(\theta)$ and $J_{\text{test}}(\theta)$ - same, but on cross-validation and test datasets respectively
Now we
- Choose a range of possible values for $\lambda$ (say 0, 0.01, 0.02, 0.04, ..., 10.24) - that gives us 12 models to checks
- For each $\lambda^{(i)}$,
- calculate $\theta^{(i)}$,
- calculate $J_{\text{cv}}(\theta^{(i)})$,
- and take $\lambda^{(i)}$ with lowest $J_{\text{cv}}(\theta^{(i)})$
After that we report the test error $J_{\text{test}}(\theta^{(i)})$
K-Fold Cross-Validation
$K$-Fold Cross-Validation If we want to reduce variability in the data
- we can perform multiple rounds of cross-validation using different partitions
- and then average the results over all the rounds
We're given a dataset $S$ sampled from the population $D$
- we partition $S$ into $K$ equal disjoint subsets $(T_1, ..., T_K)$ (typically 5-10 subsets)
- then perform $K$ steps, and at step $k$ do:
- use $R_k = S - T_k$ as the training set
- build classifier $C_k$ using $R_k$
- use $T_k$ as the test test, compute error $\delta_k = \text{error}(C_k, T_k)$
- let $\delta^* = \cfrac{1}{K} \sum_{k = 1}^K \delta_k$
- this is the expected error rate
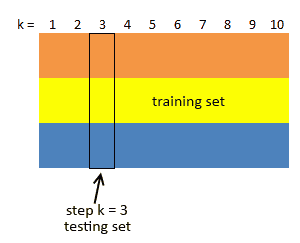
- note that there's only two subsets at each iteration
- and they are used to estimate the true error
Tuning Learning Parameter
Choosing best value for parameter $\gamma$ with $K$-Fold Cross-Validation
- you have to put some data aside before training your classifier
- i.e. split your data into learning set and test set
- for every possible value of $\gamma$
- use $K$-fold Cross-Validation to estimate the expected error rate
- use the learning set as the set $S$ (and do $K$-fold Cross-Validation only on it)
- select the optimal value of $\gamma$
- and then use the test set for the final evaluation
Stratified K-Fold Cross-Validation
What if we want to preserve the class distribution over $K$ runs?
- then for each $T_i$ pick up the same proportion of labels as in the original dataset
-
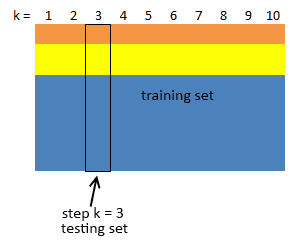
- it's very important if the test distribution is not uniform