ML Wiki
Machine Learning Wiki - A collection of ML concepts, algorithms, and resources.

System of Linear Equations

linear-algebra

System of Linear Equations

The fundamental problem of Linear Algebra is solving a system of Linear Equations.

  • A system of linear equations is a system of first order equations with multiple unknowns.

$A \mathbf x = \mathbf b$

Matrix View

Suppose we have a system with $m$ equations and $n$ unknowns:

$\left{\begin{matrix} a_{11} x_1 + a_{12} x_2 + \ … \ + a_{1n} x_n = b_1\ a_{21} x_1 + a_{22} x_2 + \ … \ + a_{2n} x_n = b_2\ \vdots
a_{m1} x_1 + a_{22} x_2 + \ … \ + a_{mn} x_n = b_m\ \end{matrix}\right.$

The coefficients of the unknowns form a Matrix - a rectangular array of numbers:

  • $A = \begin{bmatrix} a_{11} & a_{12} & … & a_{1n}\ a_{21} & a_{22} & … & a_{2n}\ \vdots & \vdots & \vdots & \vdots \ a_{m1} & a_{m2} & … & a_{mn} \end{bmatrix}$
  • We call this matrix $A$, it’s $m \times n$ matrix: with $m$ rows and $n$ columns

The unknowns themselves form a column vector $\mathbf{x}$, and the … form a column vector $b$

  • $\mathbf{x} = \begin{bmatrix} x_1
    x_2
    \vdots
    x_n
    \end{bmatrix}$, $\mathbf{b} = \begin{bmatrix} b_1
    b_2
    \vdots
    b_m
    \end{bmatrix}$,
  • they’re both column vectors, $\mathbf{x}$ has size $n$, and $\mathbf{b}$ has size $m$
  • can write them as rows using the transposition notation: $\mathbf{x} = [x_1, x_2, …, x_n]^T$ (but they still remain column vectors)

So the system of linear equations can be expressed in a matrix form as $A\mathbf{x} = \mathbf{b}$

Geometry of Linear Equations

Suppose we have the following system of linear equations:

$\left{\begin{matrix} 2x - y = 0\ -x + 2y = 3 \end{matrix}\right.$

Matrix form:

  • $\begin{bmatrix} 2 & -1 \ -1 & 2 \end{bmatrix} \begin{bmatrix} x \ y
    \end{bmatrix} = \begin{bmatrix} 0 \ 3
    \end{bmatrix}$

We can see this in two possible ways:

  • as a crossing of lines (hyperplanes) - the row picture
  • as vectors - the column picture

Row Picture

We have two lines:

  • $2x - y = 0$, $-x + 2y = 3$
  • plot them, and the point where they cross is the solution $\mathbf{x}$

Image

The solution is $[x, y]^T = [1, 2]^T$

For 3 and more dimensions, we have (hyper)planes instead of lines.

Column Picture

We have two vectors:

  • $x \begin{bmatrix} 2 \ -1
    \end{bmatrix} + y \begin{bmatrix} -1 \ 2 \end{bmatrix} = \begin{bmatrix} 0 \ 3 \end{bmatrix}$

We need to combine first two vectors $v = \begin{bmatrix} 2 \ -1 \end{bmatrix}$ and $u = \begin{bmatrix} -1 \ 2 \end{bmatrix}$ so they form $\begin{bmatrix} 0 \ 3 \end{bmatrix}$

I.e. we want to find a Linear Combination of these columns.

  • From the vector picture we know that the solution is $[1, 2]^T$, so let’s take
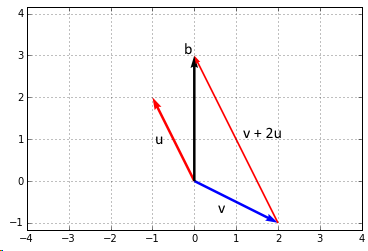
  • Image
  • so we take 1 of vector $\mathbf u$ and 2 of vector $\mathbf v$ and end up at exactly $\mathbf b$    

Python Code

Python code to reproduce the figures ```python import matplotlib.pylab as plt import numpy as np class Line: def __init__(self, slope, intercept): self.slope = slope self.intercept = intercept def calculate(self, x1): x2 = x1 * self.slope + self.intercept return x2 line1 = Line(2, 0) line2 = Line(0.5, 1.5) a = np.array([-6, 6]) plt.plot(a, line1.calculate(a), color='red', marker='') plt.plot(a, line2.calculate(a), color='blue', marker='') plt.scatter([1], [2]) plt.grid() plt.axis('equal') plt.ylim([-1, 3]) plt.xlim([-1, 3]) ``` ```python import matplotlib.pylab as plt plt.axis('equal') plt.quiver([0, 0, 0], [0, 0, 0], [-1, 2, 0], [2, -1, 3], color=['red', 'blue', 'black'], angles='xy', scale_units='xy', scale=1) plt.quiver([2], [-1], [-2], [4], color='red', width=0.005, scale=1, angles='xy', scale_units='xy') plt.grid() plt.ylim([-2, 5]) plt.xlim([-4, 4]) plt.show() ```

Solving the System

How we can solve the system $A \mathbf x = \mathbf b$?

Vector Solution: the solution found with the column picture

Matrix Solution

  • if $A$ is non-singular and invertible, then to find $\mathbf x$ multiply $\mathbf b$ by the inverse of $A$: $\mathbf x = A^{-1} \mathbf b$
  • if $\mathbf b \in C(A)$ - Column Space of $A$
    • this is especially important when the number of columns $n$ is less than the number of rows $m$

Solving $A \mathbf x = \mathbf 0$

Such systems are called ‘‘homogeneous’’ - see Homogeneous Systems of Linear Equations

Complete Solution to $A \mathbf x = \mathbf b$

Let $A$ be $n \times m$ matrix of rank $r$

  • we know that the system has a solution if $\mathbf b \in C(A)$

Steps:

  • reduce $A$ to Row Reduced Echelon Form
  • set all free variables to 0 and solve - get $\textbf x_p = \textbf x_\text{particular}$
  • then solve $A \mathbf x_n = \mathbf 0$ - get all $\mathbf x_n$ - all $\mathbf x$ that solve the homogeneous system
  • Then find all other solutions: they are $\mathbf x = \textbf x_p + \mathbf x_n$
  • this solution is called ‘‘the complete solution’’
  • why? $A \mathbf x_p = \mathbf b$ and $A \mathbf x_n = \mathbf 0$. Add them and get $A \cdot (\mathbf x_p + \mathbf x_n) = \mathbf b + \mathbf 0 = \mathbf b$
  • so we can the solution as the Nullspace $C(A)$ but shifted away from the origin by $x_p$
  • note that this solution doesn’t form a subspace

General Case, $A \mathbf x = \mathbf b$

Let $A$ be $m \times n$ matrix of rank $r$

  • $m$ - rows, $n$ - cols
  • $r \leqslant m$, $r \leqslant n$

Full Column Rank

Full rank = $r$ is as big as it can be

  • suppose that $n \leqslant m$, i.e. the number of columns is smaller than the number of rows
  • so full column rank matrix = $r = n$
  • there’s a pivot in every column, $n$ pivots $\Rightarrow$ no free variables

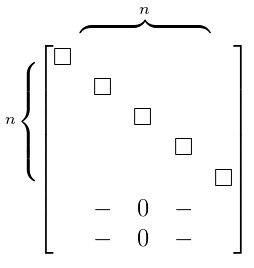
Image

Nullspace $N(A)$?

  • there are no free variables to consider
  • so $N(A) = { \ \mathbf 0 \ }$

Solution to $A \mathbf x = \mathbf b$:

  • if the solution exists (i.e. $\mathbf b \in C(A)$) then this solution is unique
  • so we have either 0 solutions or 1
  • No solution? Can approximate it with Normal Equation (That would be the Least Squares solution)

Full Row Rank

  • Now suppose that $m \leqslant n$ and $r = m$
  • so every row has a pivot, but only $r$ columns have pivots, the remaining $n - r$ don’t
  • so there are $r$ pivot columns, and $n - r$ free columns

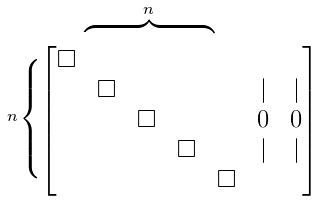
Image

for which $\mathbf b$ we can solve $A \mathbf x = \mathbf b$?

  • there are no zero rows, so can solve the system for any $\mathbf b$

Full Rank

  • If our $A$ is square, $m = n = r$
  • then there’s always a solution, and $A$ is called ‘‘invertible’’
  • $N(A) = { \ \mathbf 0 \ }$ - there’s only one unique solution

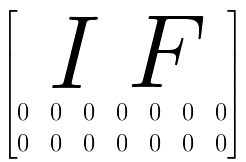
=== $r < m$ and $r < n$ === Image

  • $A \mathbf x = \mathbf 0$ always have a solution - there’s always something in the Nullspace $N(A)$ of $A$ apart from the zero-vector
  • reason: there are always free variables and we can assign any non-zero values to them and solve the homogeneous system

Zero or $\infty$ solutions

Sources

✏️ Edit on GitHub