Expected Utility Theory
We see that using Expected Value is not enough to compare simple lotteries in Decision Trees
So instead of calculating Expected Values based on (numerical) consequences, we
- replace the values of the consequences onto their utilities
- the utilities are provided by individuals - and therefore may vary from one individual to another
- the ‘‘utility’’ captures how an individual things about certain risk
Utility
- suppose we have a set of alternatives $A = {a, b, c, \ … \ }$
- utility function $U_i$ of individual $i$ is a mapping $U_i: A \mapsto X$
- where $X$ is based on numerical scale (i.e. $X \equiv \mathbb{R}$)
- we use the Weighted Sum Model to establish the final aggregated value
The preference and indifference relations are defined as follows:
- $\forall a,b \in A: a \ P \ b \iff U_i(a) > U_i(b)$ - the preference relation
- $\forall a,b \in A: a \ I \ b \iff U_i(a) = U_i(b)$ - the indifference relation
Utilities for Lotteries
- for lotteries (as defined in Decision Trees) we see the lotteries as alternatives
- probabilities are the weights
- $X$ is a set of consequences for which the lotteries are defined
The total utility:
- $U(l) = \sum_{x \in X} u(x) \cdot p_l(x)$
- where $u$ is the utility function $u: X \mapsto \mathbb{R}$ - it maps a consequence to some real number
Preference Relations
(see also Voting Theory Relations for the same ideas but in Voting Theory)
So we define the relations as:
- $l_1 \ P \ l_2 \iff U(l_1) > U(l_2)$ - the preference
- $l_1 \ I \ l_2 \iff U(l_1) = U(l_2)$ - the indifference
We also define the “as good as” relation as $S \equiv P \lor I$
- $l_1 \ S \ l_2 \iff l_1 \ P \ l_2 \lor l_1 \ I \ l_2$
Note that $S$ is transitive and consistent
- $\forall l_1, l_2, l_3 \in L(x): l_1 \ S \ l_2 \land l_2 \ S \ l_3 \Rightarrow l_1 \ S \ l_3$
$S$ alone is enough:
- $l_1 \ P \ l_2 \iff \big[ l_1 \ S \ l_2 \big] \land \big[\overline{l_2 \ S \ l_1} \big]$
- $l_1 \ I \ l_2 \iff \big[ l_1 \ S \ l_2 \big] \land \big[l_2 \ S \ l_1 \big]$
Advantages
- it’s simple
- takes individual preferences into account
- we are not restricted to numerical consequences
- there is a clear rationale why it works - the Axioms (see below)
Axioms
This is a link to Arrow’s Impossibility Theorem:
- there are 5 axioms that need to be respected
Axiom 1: Ranking
When a decision maker compares two lotteries $l_1$ and $l_2$
- he always can say if he prefers one another or he’s indifferent between them
I.e.
- $\forall l_1, l_2 \in L(X): l_1 \ S \ l_2 \lor l_2 \ S \ l_1$
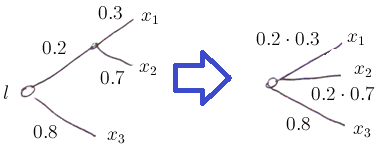
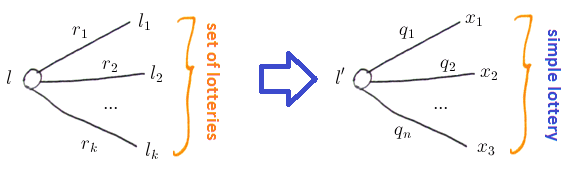
Axiom 2: Reduction
Suppose we have a high-order lottery $l$ over ${l_1, …, l_k}$
- we can always simplify $l$ and make a simple lottery from it
Example:
Axiom 3: Monotonicity
for lotteries $l_1, l_2 \in L(X)$ over the same outcomes ${x, y} \subseteq X$
- if (1) outcome $x$ is better than $y$ and (2) $p > q$
- then $l_1 \ P \ l_2$
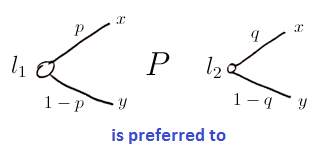
Axiom 4: Independence
for high-order lotteries $l^{(1)}, l^{(2)} \in L(X)$
- $l^{(1)}$ is over set of lotteries ${l_1, \ … \ , l_k} \subset L(X)$
- $l^{(2)}$ is over set of lotteries ${l’_1, \ … \ , l_k} \subset L(X)$
- (the sets are almost the same - they only differ in $l_1$ and $l’_1$)
- both $l^{(1)}, l^{(2)}$ have the same probability distributions over their sets
Independence:
- if $l_1 \ I \ l’_1$ then $l^{(1)} \ I \ l^{(2)}$
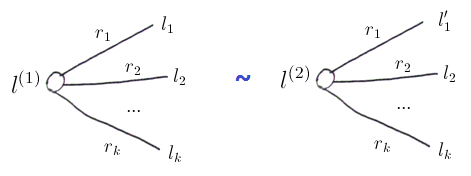
Axiom 5: Continuity
$\forall x, y, z \in X$
- if $x \ P \ y \ P \ z$ then
- there $\exists p \in [0, 1]$ s.t.
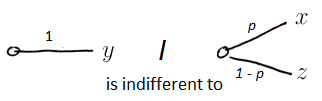
I.e.
- when something is given with certainty
- we can transform it to some lottery
Axiom 3 implies that $p$ is unique
Theorems
Representation
Let $S$ be a preference relation on $X$
- $S$ satisfies the axioms
- $\iff$
- $\exists u \ : \ X \mapsto \mathbb{R}$ for which $l_1 \ S \ l_2 \iff U(l_1) \geqslant U(l_2)$
MCDA
This principle is also used in Multi-Criteria Decision Aiding:
Links
- Axioms: http://www.intsci.ubc.ca/wiki/doku.php?id=courses:isci344:utility_theory_axioms
- The theorem: http://en.wikipedia.org/wiki/Von_Neumann%E2%80%93Morgenstern_utility_theorem