Multi-Attribute Utility Theory

Multi-Attribute Utility Theory

Multi-Attribute Utility Theory or MAUT is a method of Multi-Criteria Decision Aid

Utility Functions

Suppose we have a global utility function $U(a)$ that aggregates all criteria into one value:

• $U(a) = U(g_1(a), …, g_k(a))$

Additive Utility Functions

$U(a) = \sum_{j=1}^k u_j(g_j(a))$

• behind this we can have the Weighted Sum Model

The evaluation table:
	Price	Comfort		$a$		300	Medium		$b$		350	Good		$c$		400	Good		$d$		450	Very Good
The utility functions:
$u_1$	$u_2$		8.5	4		8	7		6	7		5	10

With weights $k_1 = 7$ and $k_2 = 3$ we establish the ranking based on the following values:

• $u(a) = 7 \cdot 8.5 + 3 \cdot 4 = 71.5$
• $u(b) = 7 \cdot 8 + 3 \cdot 7 = 77$
• $u(c) = 7 \cdot 6 + 3 \cdot 7 = 63$
• $u(d) = 7 \cdot 5 + 3 \cdot 10 = 65$
• $b > a > d > c$

Marginal Utilities

At first we transform the evaluation into two “marginal utilities”:

• we transform evaluation of all criteria into a scale $[0, 1]$

So with the weighted sum we have

• $U(a) = \sum{k=1}{n} w_k u_k(a)$
• we want $u_k \in [0, 1]$

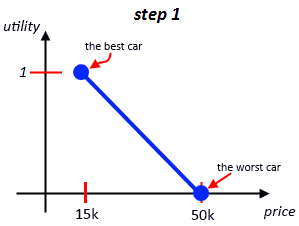
Suppose you want to buy a car

• the prices range from 15k to 50k
• so first step is assigning 1 to 15k and 0 to 50k
  • we’ve got a linear utility function
  • but this is only just the first approximation of our preferences
  • 
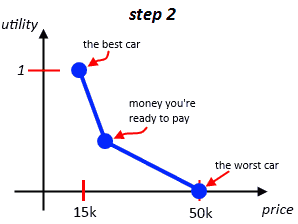
• we know that we’re willing to spend somewhere around 20k
  • we want $u(20k) = 0.5$
  • so we modify the function by adding an additional point - now there’re two linear function
  • this is the second approximation of our preferences
  • 
• can repeat this for both left and right sides to get the 3rd approximation
  • and define $u(p_1) = 0.75$ and $u(p_2) = 0.25$
  • 
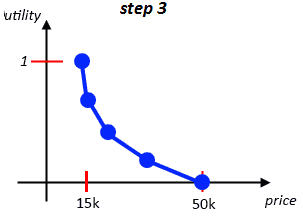
• and so on

Examples

Consider an additive model and the following evaluation table

$g_1$

$g_2$

$a_1$

1

1

$a_2$

1

3

$a_3$

1

5

$a_4$

2

1

$a_5$

2

3

$a_6$

2

5

$a_7$

3

1

$a_8$

3

3

$a_9$

3

5

Based on this table a Decision Maker gives his preferences:

• $a_9 \ P \ a_6 \ P \ a_8 \ P \ a_5 \ P \ a_3 \ I \ a_7 \ P \ a_2 \ I \ a_4 \ P \ a_1$

This ordering satisfied the Preferential Independence criteria.

Definition: $\exists a,b,c,d \in A$, and set of criteria $J \cup \overline{J} = G$

• $g_i(a) = g_i(b), \forall i \not \in J$
• $g_i(c) = g_i(d), \forall i \not \in J$
• $g_i(a) = g_i(a), \forall i \in J$
• $g_i(b) = g_i(d), \forall i \in J$

In this case $J = {g_1}, \overline{J} = {g_2}$

• under $J$: $a_1 = a_2 = a_3; a_4 = a_5 = a_6; a_7 = a_8 = a_8$
• under $\overline{J}$: $a_1 = a_4 = a_7; a_2 = a_5 = a_8; a_3 = a_7 = a_9$

Need to check if this principle is satisfied for all possible combinations

For example, $a_1, a_4, a_5, a_5$:

• $a_4 \ P \ a_1 \iff a_5 \ P \ a_2$
• this indeed holds

Now we want to check how the decision maker obtained this ranking

• can we model it with an utility function?
• note that $a_3 \ I \ a_7$
  • then under the utility model it should be true that $U(a_3) = U(a_7)$
  • $u_1(g_1(a_3)) + u_2(g_2(a_3)) = u_1(g_1(a_7)) + u_2(g_2(a_7)) = …$
  • $… = u_1(1) + u_2(5) = u_1(3) + u_2(1) \ \ \ (*)$
• also $a_2 \ I \ a_4$
  • then $U(a_2) = U(a_4)$
  • or $u_1(1) + u_2(3) = u_1(2) + u_2(1) \ \ \ (**)$
• let’s try to find the utility function
  • check $(*) - (**)$
  • $u_2(5) - u_2(3) = u_1(3) - u_1(2) \Rightarrow u_1(2) + u_2(5) = u_1(3) + u_2(3)$
  • we see that $a_6$ is evaluated to $(2, 5)$ and $a_8$ is evaluated to $(3, 3)$
  • but it means that we should also have $a_6 \ I \ a_8$ - which is not the case
  • thus it’s not possible to establish

Sources

• Decision Engineering (ULB)