ML Wiki

Graph Kernel

A kernel of a graph $K \subset V$ is ($V$ - all nodes of a graph)

• $\forall a \in K, \not \exists b: a \to b$

  no alternative $a$ inside the kernel $K$ is better than any other alternative $b$ inside $K$

• $\forall c \not \in K, \exists a \in K: a \to c$

  each alternative $c$ outside of the kernel $K$ is worse than at least one alternative $a$ inside $K$

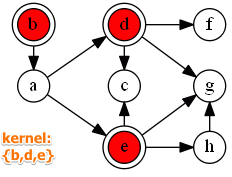
For the example above:

• $K = \{b, d, e\}$
• 

Remarks:

• If the graph has no cycles then the kernel is unique
• Each cycle can be replaced by a single node (see Strongly Connected Components)

Usage

• ELECTRE methods of MCDA.

Links

• http://en.wikipedia.org/wiki/Graph_kernel
• http://jmlr.org/papers/volume11/vishwanathan10a/vishwanathan10a.pdf

Sources

• Decision Engineering (ULB)
• http://web.itu.edu.tr/~topcuil/ya/MDM08Outranking.pptx
• http://electre.no.sapo.pt/MElecI2.htm