ELECTRE

multi-criteria-decision-aid

ELECTRE

This is a method from the family of outranking (i.e. based on pair-wise comparison) MCDA methods. The result is a partial ordering of alternatives (see Partial Order Preference Structure)

Here:

ELECTRE I

ELECTRE I chooses alternatives that are preferred by the majority of the criteria and which don;t cause an unacceptable level of discontentment on other criteria.

Preferences

; Main idea:

When we say $a \ P \ b$?

(1) if we have a lot of criteria for which $u_i(a) > u_i(b)$ (where $u_i$ - some utility function)
(2) and we have no strong arguments that say the opposite of (1)

The ELECTRE methods are based on two concepts:

Concordance Index
Discordance Index

Concordance Index

Or quantification of positive arguments

For ELECTRE 1, when comparing $a$ and $b$

identify all criteria $g_j$ such that $g_j(a) \geqslant g_j(b)$
for all such criteria $g_j$ sum their weights $w_j$,
let $W$ be the sum of all weights: $W = \sum_i w_i$ (we use this for normalization)
define the concordance index as:
: $c(a, b) = \cfrac{1}{W} \sum_{j: g_j(a) \geqslant g_j(b)} w_j$

Note that weight should sum up to 1

There are two extreme cases:

$c(a, b) = 1$: all criteria for $a$ are better than for $b$ (Unanimity)
- have very good reasons to say $a \ P \ b$
$c(a, b) = 0$: there is no criteria in which $a$ better than $b$

Discordance Index

Or quantification of negative arguments

We want to find a strong argument against $a \ P \ b$

if we find such an argument then we cannot say that $a \ P \ b$

For ELECTRE I, define $d(a, b)$ as

0 when $\forall j: g_j(a) \geqslant g_j(v)$ (none when there’s Unanimity)
if $\exists g_i: g_i(b) \geqslant g_i(a)$ then we have an argument against $a \ P \ b$
in this case we want to identify the largest difference between $a$ and $b$:
- $\cfrac{1}{\delta} \max_j [g_j(b) - g_j(a)]$
- $\delta$ is normalization factor: $\delta = \max_{i,c,d} [g_i(c) - g_i(d)]$

Another way

let $D$ be the set of cases where we list cases that cannot be compared
if for a pair of alternatives $(a, b)$ there exists a criteria $g_i$ s.t. $(g_i(a), g_i(b)) \in D$ then we cannot compare these alternatives

Outranking Preference Relation

For ELECTRE I we define $S \equiv P \lor I$ as: (the “as good as relations”, also see Voting Theory Relations)

$a \ S \ b \iff$
- (1) $c(a, b) \geqslant \tilde c$
- : a lot of positive arguments to say $a \ S \ b$
- (2) $d(a, b) \leqslant \tilde d$
- : not many negative arguments to say the opposite
so for that we also have to provide two parameters:
- $\tilde c$ - the ‘‘concordance threshold’’ and $\tilde d$ - the ‘‘discordance threshold’’

Or:

$a \ S \ b \iff$
- (1) $c(a, b) \geqslant \tilde c$
- (2) $\forall g_i: \big(g_i(a), g_i(b)\big) \not \in D$

Note that this relation gives us partial order:

we have $P$ and $I$ (expressed via $S$)
and we have $J$ (when discordance threshold is exceeded)

Graph Kernels

Graph Kernels are used to identify good alternatives.

It is possible to express the outranking relation $S$ in form of a directed graph

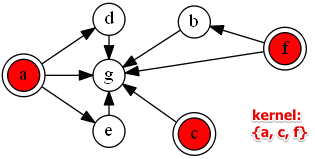
Example:

$a$ is better than $e$ and $d$
$d$ is better than $f$ and $c$
etc

A ‘‘kernel’’ of a graph $K \subset A$ is

$\forall a \in K, \not \exists b: a \ S \ b$
: no alternative $a$ inside the kernel $K$ is better than any other alternative $b$ inside $K$
$\forall a,b \in K: a \ ? \ b$
: within the kernel we cannot say anything about the relation between $a$ and $b$
$\forall c \not \in K, \exists a \in K: a \ S \ c$
: each alternative $c$ outside of the kernel $K$ is worse than at least one alternative $a$ inside $K$

For the example above:

$K = {b, d, e}$

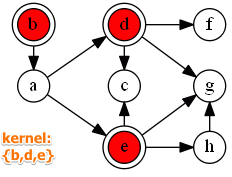
Another example

Remarks:

If the graph has no cycles then the kernel is unique
Each cycle can be replaced by a single node (see Strongly Connected Components)

The kernel $K$ of a set $A$ forms a set of preferred alternatives.

Examples

Example 1

| | price | comfort | speed | aesthetic | | 1 | 300 | ex | fast | good | || 2 | 250 | ex | med | good | || 3 | 250 | med | fast | good | || 4 | 200 | med | fast | med | || 5 | 200 | med | med | good | || 7 | 100 | poor | med | med | || $w$ | 5 | 4 | 3 | 3 | $W = \sum w = 15$ |

Concordance

Perform pair-wise comparisons for all elements $A$

let’s compare (1) and (2)
concordance: $c(1, 2) = \cfrac{1}{15} (4 + 3 + 3) = \cfrac{2}{3}$

This way we compare each with each:

| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 1 | - | 10 | 10 | 10 | 10 | 10 | 10 || 2 | 12 | - | 12 | 7 | 10 | 7 | 10 || 3 | 11 | 11 | - | 10 | 10 | 10 | 10 || 4 | 8 | 8 | 12 | - | 12 | 12 | 10 || 5 | 8 | 11 | 12 | 12 | - | 12 | 10 || 6 | 11 | 11 | 11 | 11 | 11 | - | 10 || 7 | 5 | 8 | 5 | 8 | 8 | 9 | - | (note that this is not normalized - need also to divide on 15)

Discordance

In this case we define discordance by enumerating cases that are forbidden

The following tables shows what veto we define

price

comfort

$a$

250

poor

$b$

100

excellent

Graph

So the establish the following relation $S$ and the following graph:

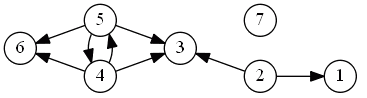
There are two kernels in this case:

2, 4, 7
:
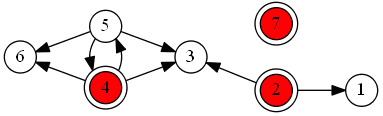
2, 5, 7
:

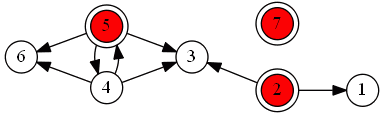
Kernel:

6 is dominated - remove it
same for 3 and 1
since there’s a cycle we have to decide between 4 and 5, and remove one of them
when we put alternatives into a kernel, it doesn’t mean they are the best, but it means it allows to apply the Dominance principle and remove dominated alternatives

Example 2

A company wants to rank 5 candidates $A,B,C,D,E$ for a promotion
Criteria:
- Reputation of diploma $D$
- Skills $K$
- Personality $P$
- Spoken Languages $L$
- Seniority $S$
Apply ELECTRE with concordance threshold 0.6 and discordance 6

The following evaluation table is obtained

| | $A$ | $B$ | $C$ | $D$ | $E$ | Weight | $D$ | 7 | 11 | 15 | 11 | 16 | 15 || $K$ | 12 | 18 | 6 | 8 | 10 | 15 || $P$ | 13 | 13 | 14 | 19 | 10 | 15 || $L$ | 18 | 16 | 19 | 13 | 19 | 25 || $S$ | 10 | 20 | 16 | 14 | 20 | 20 | Total weight is $W = 15 + 15 + 15 + 25 + 20 = 100$

Concordance

Then we construct the concordance index by comparing alternatives pair-wise

For example, consider alternatives $A$ and $B$

| | $A$ vs $B$ | $B$ vs $A$ | $D$ | | 15 || $K$ | | 15 || $P$ | 25 | 25 || $L$ | 25 | || $S$ | | 20 || ‘'’Total’’’ | 50 | 100 || ‘'’Normalized’’’ | 0.5 | 0.75 | Repeating this for all pairs, construct the following table:

$A$

$B$

$C$

$D$

$E$

$A$

’'’0.75’’’

0.15

0.4

$B$

0.5

0.35

’'’0.75’’’

’'’0.6’’’

$C$

’'’0.85’’’

’'’0.65’’’

’'’0.6’’’

0.5

$D$

’'’0.6’’’

0.25

0.4

0.25

$E$

’'’0.6’’’

’'’0.75’’’

’'’Bold’’’ are alternatives that should be preferred provided that there’s no discordance

recall that $\tilde c = 0.6$ and we check all values that $\geqslant \tilde c$

Discordance

The discordance index is $\tilde d = 6$

we don’t normalize on $\delta$ here because our values are already normalized

Let’s compare $A$ with $B$ and $A$ with $C$:

| | $A$ vs $B$ | $B$ vs $A$ | $A$ vs $C$ | $C$ vs $A$ | $D$ | 7 | - | ‘'’8’’’ | - || $K$ | 6 | - | - | ‘'’6’’’ || $P$ | 0 | 0 | 1 | - || $L$ | - | ‘'’2’’’ | 1 | - || $S$ | ‘'’10’’’ | - | 6 | - || ‘'’Max’’’ | ‘‘10’’ | 2 | ‘‘8’’ | ‘‘6’’ || Rel | $A \ J \ B$ | | $A \ J \ C$ | $C \ J \ A$ |

if a difference exceeds the threshold, the alternatives are incomparable

Graph

Based on the Concordance and Discordance we define the outranking relation $S$

this relation can be depicted as a graph

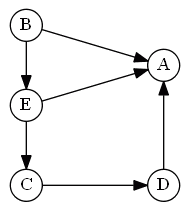
Sources

Decision Engineering (ULB)
http://web.itu.edu.tr/~topcuil/ya/MDM08Outranking.pptx
http://electre.no.sapo.pt/MElecI2.htm
Multiple Criteria Decision Analysis: State of the Art Surveys, 2005

✏️ Edit on GitHub