Linear Hashing
- another dynamic hashing schema
- but without a directory that doubles in size as in Extensible Hashing
Variables we use
- $b$ - length of bit-string that Hash Function outputs (typically 64)
- $i$ - number of bits we can use
- as number of keys grows, we increase $i$
- but in contrast to Extensible Hashing, we use $i$ ‘‘least’’ significant bits if key
- for example, $\overbrace{0 1 1 1 0 \underbrace{1 0 1 1}_{i}}^{b}$ with $i$ = 4 and $b$ = 9
- $n$ - number of buckets we use now, $n \leqslant 2^i$
- $2^i$ - max number of items we can address with current $i$
- $n$ grows linearly
Lookup Rule
- if $\underbrace{h(k)[i..b]}_{\text{$i$ least significant bits}} \leqslant n$
- then look at bucket $h(k)[i..b]$
- otherwise look at the bucket $h(k)[i..b] - 2^{i - 1}$ (i.e. just flip the most significant bit of the hash)
- this rule is used for inserting and looking up
’'’Example’’’
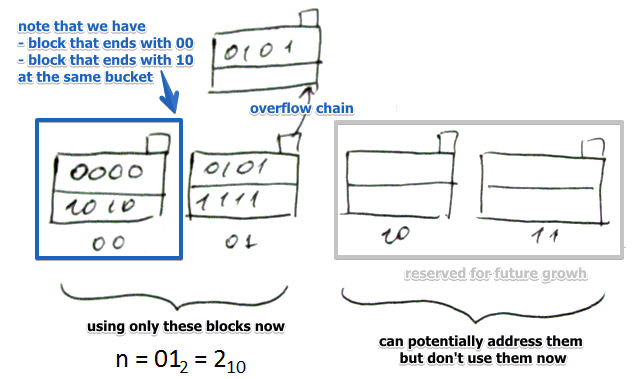
- $b$ = 4 bits
- $i = 2$, can address $2^i = 4$ buckets
- $n = 012 = 2{10}$ i.e. we use only two buckets at the moment
- the remaining 2 buckets are reserved for future growth
- note that in the first bucket there are 2 values: 0000 (2 last bits are $00$) and 1010 (with $10$)
- they are different but ended up in the same bucket
- since $10_2 \leqslant n = 01_2$ we flip the first significant bit of $10$ and get $00$
- also we allow overflow blocks for this data structure
Increasing Parameters
Increasing $n$
- when we increase $n$ we start using a new block
- and we need to re-organize data so the #Lookup Rule invariant is maintained
- if there’s an overflow block, we will reduce it
Reorganization
- for that we see the block with current $n$ but most significant bit flipped
- i.e. for $10$ it’s $00$
- then we go through all records there and move those that should belong to new block $10$
- after doing that the Lookup Rule invariant will be maintained
Increasing $i$
If we increase $i$
- now number of buckets we can address becomes two times higher
- nothing will move: we don’t touch $n$
- but $i$ gets increased only when $n$ increases, but doesn’t fit to current $i$
When
When it’s better to increment $n$?
- Similar to ideas from Open Hashing Index
- $u = \cfrac{\text{# records}}{\text{# buckets}}$ where $u$ is ‘‘space utilization’’
- and we set some threshold - once we exceed it, we increment $n$
- $i$ is incremented when $n$ becomes high enough so it no longer fits in $i$ bites
Algorithm
When increasing $n$
- $n \leftarrow n + 1$
- if $n > i$, then $i \leftarrow i + 1$
- let $k$ be equal to $n$ with first significant bit flipped
- look for all keys that end with $n$ in the bucket #$k$
- and move them to the new bucket
- remove overflow blocks when needed
Example
$b = 4$
Growing $n$
- suppose we have 2 blocks not in use, $n = 01$, $i = 2$
- we increase $n$: $n \leftarrow 10$
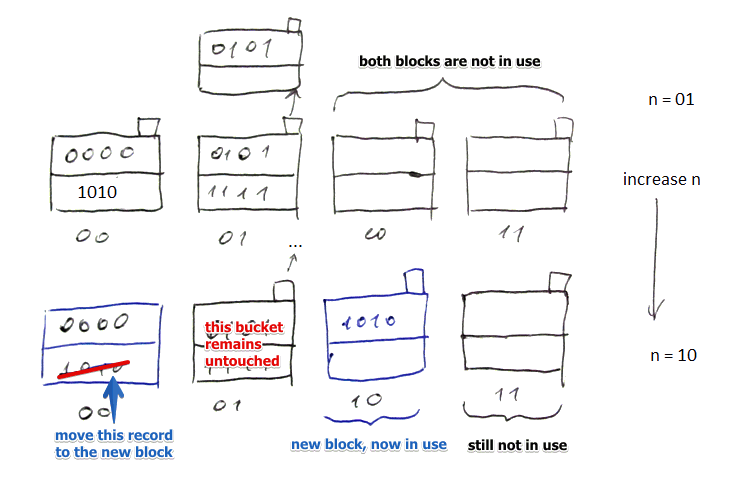
- we transfer one record from 00 to 10 (which now becomes in use)
Removing overflow blocks
- suppose now we increase $n$ again: $n \leftarrow 11$
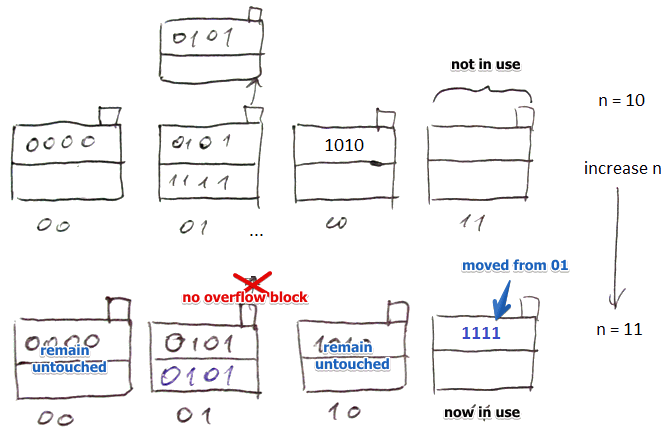
- we transfer records from 01 to 11
- we move record 1111 to the new block
- since now there’s some free room, we move records from the overflow block
- after moving them the overflow block becomes empty - so we may remove it altogether
note that in all cases we need to reorganize at most one bucket
Increasing $i$
- nothing moves as long as we don’t touch $n$
- just append zeros before old bucket numbers + add new ones
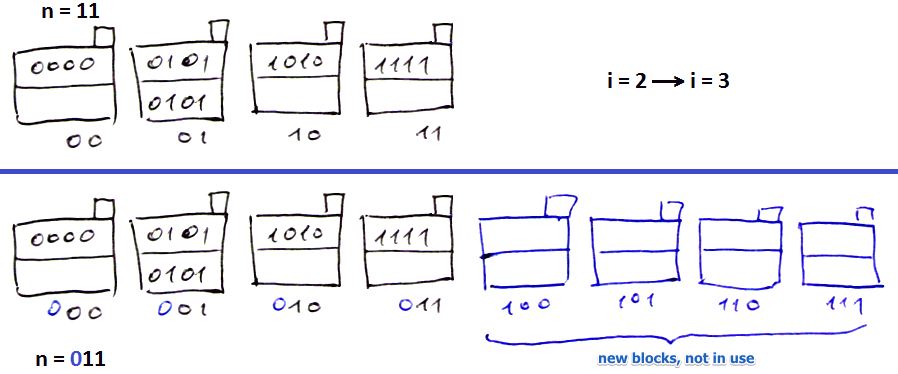
- now can increase $n$ again
Summary
- Can handle growing files (+)
- No additional level of indirection like in Extensible Hashing (+)
- Can still have overflow chains (-)
Very Bad Case
- suppose for block $011$ we have huge overflow chain
- to reconstruct this chain, $n$ has to reach $111$ (twice more| ) |- lots of time| especially when $i$ becomes longer | |
See also
- Open Hashing Index
- Extensible Hashing