Open Hashing Index

Open Hashing Index

Idea:

• apply Open Hashing to Secondary Storage to build an index

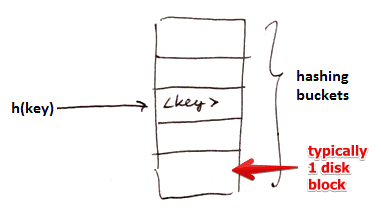
Given:

• We have $n$ hashing buckets (each bucket is typically one disk block)
• a Hash Function $h$ that maps a key $k$ to a bucket: an integers $\in [0 .. n - 1]$

Examples

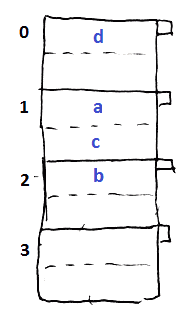
• assume we have 2 records per bucket
• hash function: $h(a) = 1, h(b) = 2, h(c) = 1, h(d) = 0$

Storing

Two options

• store records themselves in the buckets (clustered index)
• store only pointers to actual records (the only option for secondary index) (unclustered index)
• 
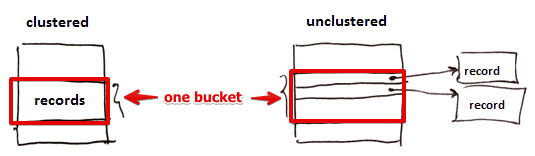
• also see (Clustered Index)

Do we sort records by key withing buckets

• we may if we want faster retrieval
• and inserts and deletes are not frequent (they get slower)

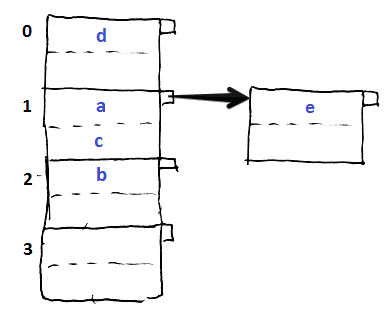
Overflow Blocks

We allow overflow blocks

• when we want to insert something, but there’s no room in the bucket
• 

Operations

Lookup

• for a search key $k$ calculate $h(k)$ (apply hash function to the key)
• use the returned value to locate the bucket with our record
• if the record is not there we follow the overflow pointer
• once we’ve reached the end of chain and still haven’t found anything - there is no such record

Insert

• suppose we want to insert $e, h(e) = 1$
• but bucket 1 is already full
• we create an overflow block and put it there
• 

Algorithm

• calculate $h(k)$ to locate bucket $B$ to use
• if $B$ is not full, just add
• if $B$ is full, and there’s an overflow block, try putting it there
• otherwise create a new overflow and store this record there

’'’NB:’’’ performance degrades as the number of overflow blocks grows| see #Reorganization | |

Deletion

• for search key $k$ calculate $h(k)$ to locate the bucket $B$
• find the record in bucket $B$
• if there not there - follow the overflow pointer
• if there - remove it
• if you’re in an overflow block and this record was the last one - also remove the block
• if not last one - you may want to shift elements from other overflow blocks

Reorganization

Rule: we want to keep space utilization between 50% and 80%

'’space utilization’’ - how much space is used

• $u = \cfrac{\text{# keys used}}{\text{total # of keys}}$
• the denominator is the # of keys that we can store if we used ‘'’only’’’ main buckets, without any overflow blocks
  • e.g. 2 items per block, 3 blocks = 6 keys
• if $u < 50\%$ - lots of space wasted (many empty buckets)
• if $u > 80\%$ - significant overflow
• if we go beyond the boundaries, we need to do rehashing

Rehashing: creating new buckets or eliminating wasted space

• very costly

Other Hash-Based Indexes

To be able to better cope with growth, there are other approaches:

• Dynamic Hashing:
  • Extensible Hashing
  • Linear Hashing

See also

• Indexing (databases)
• http://dblab.cs.toronto.edu/courses/443/2013/06.hash-index.html

Sources

• Database Systems Architecture (ULB)