Extensible Hashing
Hash-based secondary memory index structure for databases
Main ideas:
- Growing hash function
- Directory
Growing Hash Function
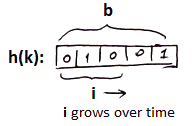
Variables we use:
- $b$ - length of bit-string that Hash Function outputs (typically 64)
- $i$ - number of bits we can use
- as number of keys grows, we increase $i$
Directory
'’Directory’’ introduces additional level of indirection
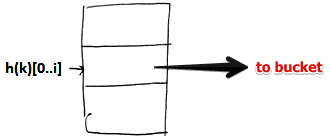
- here we keep all possible combinations of $i$ bits with pointers to associated buckets
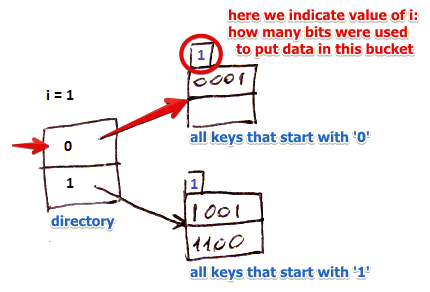
Example
- suppose for key $k$: $h(k) = \fbox{1010}$
- we take first $i$ bits of this value, i.e. $h(k)[0..i] = 1$
- so we find record with 1 in the directory and this way we locate the needed bucket
Operations
Lookup
- we take first $i$ bits of hash and find a corresponding record in the directory
- then we follow the pointer and find the whole key (all $b$ bits) there
=== Insert ===
Simple Case
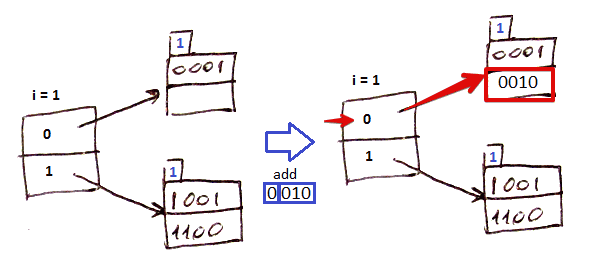
- suppose $i = 1$
- for key $k:$ $h(k) = 0010$ and first $i$ bits are 0: look it up in the directory
- follow the pointer
- there is enough room so add in there
Creating New Directory
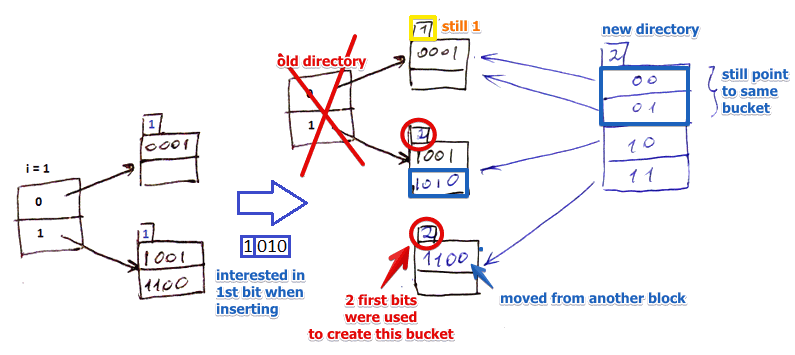
- suppose $i = 1$
- given hash $h(k) = 1010$ we extract first 1 bit which is 1
- we look 1 up in the directory and follow the pointer
- but there’s no room in this block
- so we split it into 2 parts
- keep ones that start with 10 in one
- and move ones that start with 11 to another
- that means that both blocks use 2 bits to assign a key to a bucket (and we indicate that value on top of the buckets)
- but to address these new buckets now we need 2 bits, and still $i = 1$
- i.e. $i$ in the directory becomes less than at least one $i$ from buckets
- that means we need to ‘'’create a new directory’’’
- if it wasn’t the case, we just would re-wire pointers to the dict
- note that bucket for (0) is still the same - so both 00 and 01 in the new directory point to this bucket
- if now we insert 0000 and 0100, we will reorganize the first bucket, but will not rebuild the directory
So the rule is:
- if $i$ for one of the bucket grows more than $i$ of the directory
- we need to rebuild the prefix directory
- all other blocks are kept untouched (otherwise we would have to re-organize the whole thing)
Deletion
Just the opposite of #Insertion
Summary
Pros
- can handle growing files with less wasted space than Open Hashing Index
Cons
- another level of indirection. Not that bad if we can store the entire directory in memory, but it’s not often the case
- size of directory growth is exponential to $i$ - quickly becomes the bottleneck and may introduce a lot of latency
- it fits into memory and then all of a sudden it doesn’t
Linear Hashing is another alternative that can handle growing files better