Regression
How to understand the linear relationship between data?
- dependent (response) variable - $Y$
- independent (explanatory) variable or predictor - $X$
To what extent $X$ can help us to predict $Y$?
Regression Line
The line has the followoing form:
- $y = b_0 + b_1 \cdot x$
- $b_0$ - intercept
- $b_1$ - slope
Suppose we have $n$ observations
- for $i$th observation we have $y_i = b_0 + b_1 x_i$
- and difference $y_i - b_0 - b_1 x_i$ is called ‘‘residual’’
- We’d like to make these differences for all $i$ as small as possible
Method of Least Squares
To find the slope and the intercept parameters we may use the method of least squares
Interpretation
- Suppose we have $b_0 = -23.3, b_1 = 0.41$
-
- It means that
- When $X$ increases by 1, $Y$ increases by 0.41
-
- $b_0$ value the regression would give if $X = 0$
- or how much we have to shift the line
Symmetry
- Regression is not symmetric:
- regressing $X$ over $Y$ is not the same as regressing $Y$ over $X$
Example
This is an example of best linear fit:
<img src=”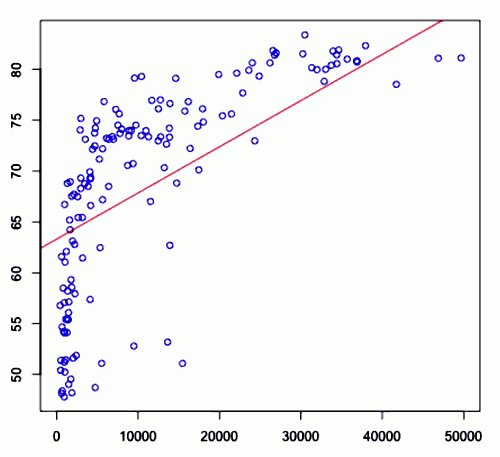 ” />
” />
Correlation
For intercept we have:
- $b_0 = \cfrac{1}{n} (\sum y_i - b_1 \sum x_i) = \bar{y} - b_1 \bar{x}$
So the regression line takes the following form
- $b_0 + b_1 x_i = (\bar{y} - b_1 \bar{x}) + b_1 x_i = \bar{y} + b_1 (x_i - \bar{x})$
This means:
- we start from mean of $y$
- and shift by how far we’re from $\bar{x}$ multiplied by slope
- $(\bar{x}, \bar{y})$ is always on the line| | | Let’s manipulate it a bit the formula for the slope coefficient to get better understanding of what’s going on
- $b_1 = \cfrac{n \sum x_i y_i - \sum x_i \sum y_i }{n \sum x_i^2 - (\sum x_i)^2} $ (divide top and bottom by $1/n^2$)
- $ = \cfrac{\frac{1}{n} \sum x_i y_i - \frac{1}{n} \sum x_i \cdot \frac{1}{n} \sum y_i}{\frac{1}{n} \sum x_i^2 - (\frac{1}{n} \sum x_i )^2 } $
- $= \cfrac{\frac{1}{n} \sum x_i y_i - \bar{x} \bar{y}}{\frac{1}{n} \sum x_i^2 - \bar{x}^2 } $
- $ = \cfrac{\frac{1}{n} (x_i - \bar{x})(y_i - \bar{y}) }{\frac{1}{n} \sum (x_i - \bar{x})^2 }$ (let’s multiply top and bottom on $\sqrt{\sum (y_i - \bar{y}) }$)
- $ = \cfrac{(x_i - \bar{x})(y_i - \bar{y}) \cdot \sqrt{\sum (y_i - \bar{y})^2 } }{ \sqrt{\sum (x_i - \bar{x})^2 } \cdot \sqrt{\sum (x_i - \bar{x})^2 } \cdot \sqrt{\sum (y_i - \bar{y})^2 }} = R \cfrac{s_y}{s_x}$
- So we get
- $b_1 = R \cfrac{s_y}{s_x}$
where
- $s_x = \sqrt{\cfrac{1}{n - 1} \sum (x_i - \bar{x}) }$ and
- $s_y = \sqrt{\cfrac{1}{n - 1} \sum (y_i - \bar{y}) }$
- $R = \cfrac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2 \sum (y_i - \bar{y})^2 }}$ is the '’correlation coefficient’’
Residuals
'’Residuals’’ is the difference between actual values and predicted values
$i$th residual is:
- $e_i = y_i - (b_0 + b_1 x_i) = y_i - b_0 - b_1 x_1 $
Residual Analysis
Residual Analysis - is a powerful mechanism for estimating how good a regression is
- It gives us $R^2$, called Coefficient of Determination, which is a measure of how much variance in the data was explained by our regression model
Regression Inference
How much uncertainty is it there? Can we apply
We have a formula for slope $b_1$ and, let $\beta_1$ be the true value of slope
- How close $b_1$ to $\beta_1$?
There’s the following fact:
- $\cfrac{b_1 - \beta_1}{\text{SE}(b_1)} \sim t_{n - 2}$
- where $\text{SE}$ is ‘‘standard error’’
- we loose one degree because we don’t know the slope and the other because of the intercept
And we calculate the standard error as
- $\text{SE}(b_1) = \cfrac{\sqrt{\sum e_i^2 }}{\sqrt{(n - 2) \sum (x_i - \bar{x})^2 } }$
- recall that $e_i = y_i - (b_0 + b_1 x_i)$
Confidence Intervals
- So a $(1 - \alpha)$ CI for $\beta_1$ is
- $b_1 \pm T_{\alpha/2, n-2} \cdot \text{SE}(b_1)$
Example
- $Y$ = age difference
- $X$ = bmi
- $n = 400$
- $b_1 = 0.41$
- $\sum e_i^2 = 78132$
- $\sum(x_i - \bar{x}) = 8992$
We’re interested to calculate 95% CI:
- $0.41 \pm 1.97 \cdot \cfrac{\sqrt{78131}}{\sqrt{398 \cdot 8992}} = 0.41 \pm 0.29 = [0.12, 0.70]$
Hypothesis Testing
We may want to ask if there is any linear relationship.
So the following test gives an answer:
- $H_0: \beta_1 = 0, H_A: \beta_1 \neq 1$
For the example above we have
- $\cfrac{b_1 - \beta_1}{\text{SE}(b_1)} \sim t_{n - 2}$
- $b_1= 0.41, \text{SE}(b_1) = 0.148$
$p$-value (under $H_0$)
- $P( | b_1 - \beta_1 | \geqslant 0.41 ) = $ |- $P \left( \left| \cfrac{b_1 - \beta_1}{\text{SE}(b_1)} \right| \geqslant \cfrac{0.41}{\text{SE}(b_1)} \right) \approx$ |- $P( | t_{398} | \geqslant 2.77 ) \approx 0.0059$ | Quite small, so we reject the $H_0$ and conclude that $\beta_1 \neq 0$, i.e. there is some linear relationship.
Limitations
-
linear - fails to predict other kinds of relationships (quadratic etc) - not robust to outliers (just one outlier can change the regression line rather significantly)
Gradient Descent
Another way of finding the slope and intercept parameters is Gradient Descent Algorithm,
- which, usually, gives approximate solution,
- but works faster for Multivariate Linear Regressions
Multivariate Linear Regression
We can use the regression to fit a linear model for several variables.
In R
```cbm basic v2
- lm - linear model lm1 = lm(diff ~ bmi)
plot(diff ~ bmi) abline(lm1)
-
summary of regression summary(lm1)
-
the residual difference for each observation lm1$residuals ```
Logarithmic transformation
text only
lm1 = lm(diff ~ log10(bmi))