Gradient Descent
Suppose we have a cost function $J$ and want to minimize it
- say it takes 2 parameters $\theta_0$ and $\theta_1$
- So we have $J(\theta_0, \theta_1)$ and want to find $\min_{\theta_0, \theta_1} J(\theta_0, \theta_1)$
Idea:
- start with some $(\theta_0, \theta_1)$ (say, $(0,0)$)
- keep changing $(\theta_0, \theta_1)$ to reduce $J(\theta_0, \theta_1)$ until we end up in minimum
In the pseudo code
- repeat until converges
- for $j = 0$ and $j = 1$
- $\theta_j = \theta_j - \alpha \cfrac{\partial}{\partial \theta_i} J(\theta_0, \theta_1)$
$\alpha$ is the learning rate, value that specifies how small are steps we take
Simultaneous Update
Note that the update for $(\theta_0, \theta_1)$ has to be ‘‘simultaneous’’. That is
- $\tau_0 = \theta_0 - \alpha \cfrac{\partial}{\partial \theta_0} J(\theta_0, \theta_1)$
- $\tau_1 = \theta_1 - \alpha \cfrac{\partial}{\partial \theta_1} J(\theta_0, \theta_1)$
- $\theta_0 = \tau_0$
- $\theta_1 = \tau_1$
As you see, $\theta_0$ is used to calculate new value for $\theta_1$, so we cannot update it before we calculate new value for $\theta_0$.
This is called ‘‘simultaneous update’’
Intuition
Let’s see how it works
- assuming that there’s only one variable $\theta_1$ and $\theta_1 \in \mathbb{R}$
$\theta_1 = \theta_1 - \alpha \cfrac{d}{d \theta_1} J(\theta_1)$
let’s have a look at the partial derivative:
- $\beta = \alpha \cfrac{d}{d \theta_1} J(\theta_1)$
if the derivative is positive
- <img src=”
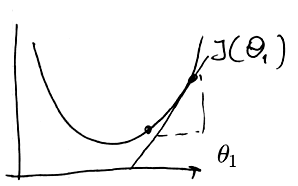 ” />
” /> -
- we’re moving left:
- $\theta_1 = \theta_1 - \beta$
if the derivative is negative
- <img src=”
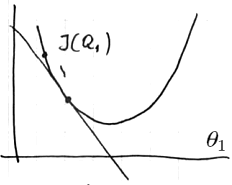 ” />
” /> -
- we’re moving right:
- $\theta_1 = \theta_1 + \beta$
- For two variables the cost function would look like that:
- <img src=”
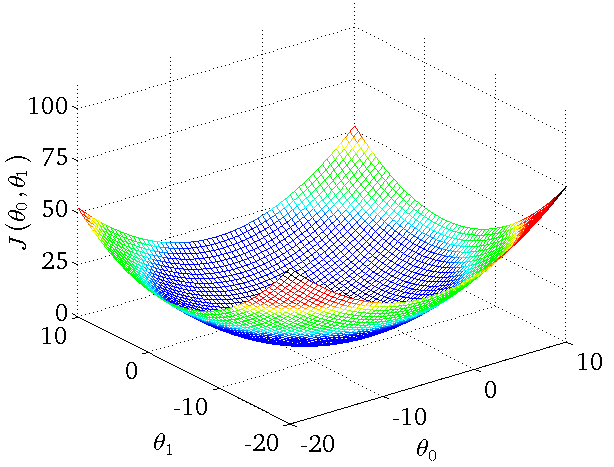 ” />
” />
Learning Rate
- when $\alpha$ is too small - we’re taking very small steps - too slow
-
- when $\alpha$ is too large - we’re taking too big steps and may miss the minimum
-
in this case not only may it fail to converge, but even diverge Approaching the minimum
- As we’re approaching the local minimum, it takes smaller and smaller steps
- If $\theta_1$ is at the local minimum, then $\beta = 0$ and $\theta_1$ won’t change
Convex Function
The cost function $J$ has to be convex if we don’t want to end up in a local minimum.
Univarivate Linear Regression
- Given input data set ${(x^{(i)}, y^{(i)}}$ of size $m$
- We have our hypothesis $h(x) = \theta_0 + \theta_1 x$
- how to choose $\theta_0$ and $\theta_1$ so $h(x)$ is closest to the set of input data
We need to minimize the cost function:
- $J(\theta_1, \theta_2) = \cfrac{1}{2 m} \sum_{i = 1}{m} (h_0 x^{(i)} - y^{(i)} )^2$
- This is the ‘‘squared error cost function’’
- Let’s simplify our expression:
- $\cfrac{\partial}{\partial \theta_j} J(\theta_0, \theta_1) = \cfrac{\partial}{\partial \theta_j} \cfrac{1}{2m} \sum (h_{\theta}(x^{i}) - y^{(i)} )^2 = \cfrac{\partial}{\partial \theta_j} \cfrac{1}{2m} \sum (\theta_0 + \theta_1 x^{i} - y^{(i)} )^2 $
Now we calculate the derivatives and have:
-
- for $\theta_0$:
- $\cfrac{\partial}{\partial \theta_0} J(\theta_0, \theta_1) = \cfrac{1}{m} \sum (h_{\theta} (x^{(i)}) - y^{(i)})$
-
- for $\theta_1$:
- $\cfrac{\partial}{\partial \theta_1} J(\theta_0, \theta_1) = \cfrac{1}{m} \sum (h_{\theta} (x^{(i)}) - y^{(i)}) \cdot x^{(i)}$
So for the regression the algorithm is
- repeat until converges
- $\theta_0 = \theta_0 - \alpha \cfrac{\partial}{\partial \theta_0} J(\theta_0, \theta_1) = \cfrac{1}{m} \sum (h_{\theta} (x^{(i)}) - y^{(i)})$
- $\theta_1 = \theta_1 - \alpha \cfrac{\partial}{\partial \theta_1} J(\theta_0, \theta_1) = \cfrac{1}{m} \sum (h_{\theta} (x^{(i)}) - y^{(i)}) \cdot x^{(i)}$
- (update simultaneously)
The square error cost function is convex, so we always converge to the global minimum.
Gradient Descent for Multivariate Linear Regression
For Multivariate Linear Regression we have $x^{(i)} \in \mathbb{R}^{n + 1} $and $\theta = \in \mathbb{R}^{n+1}$, where
- $n$ - is number of features
- $m$ - number of training examples
- and $x_0^{(i)} = 1$ for all $i$ (the slope)
- So out cost function takes the following form:
- $J(\theta) = J(\theta_0, … , \theta_n) = \cfrac{1}{2m} \sum_{i = 1}^{m} (h_{\theta} (x^{(i)}) - y^{(i)} )^2$
The algorithm:
- repeat
- simultaneously for all $i$
- $\theta_j = \theta_j - \alpha \cfrac{\partial}{\partial \theta_j} J(\theta)$
or, having calculated the derivatives:
- repeat
- simultaneously for all $i$
- $\theta_j = \theta_j - \alpha \cfrac{1}{m} \sum (h_{\theta}) (x^{(i)}) - y^{(i)} ) \cdot x_j^{(i)}$
Gradient Descent in Practice
Feature Scaling
Use Feature Scaling to help GD converge faster
Learning Rate
- How to choose $\alpha$?
- If GD works properly, cost function should decrease after each iteration
- if $J$ decreases by less than $\epsilon = 10^{-3}$ in one iteration - declare ‘‘convergence’’
- If $J$ is increasing instead - need to make $\alpha$ smaller
Choosing $\alpha$:
- But don’t choose $\alpha$ too small - it’ll take too long to converge
-
- To choose $\alpha$ try
- $…, 0.001, 0.01, 0.1$, … or increase it 3-fold
- And see what is acceptable
Applications
Apart from Linear Regression, Gradient Descent may also be used for
- Logistic Regression
- Neural Networks
- and many others