ML Wiki
Machine Learning Wiki - A collection of ML concepts, algorithms, and resources.

Matrix-Matrix Multiplication

linear-algebra

Matrix-Matrix Multiplication

Suppose we want to multiply $m \times n$ matrix $A$ on $n \times p$ matrix $B$, we get an $m \times p$ matrix $C$

Linear Transformation

What is matrix-matrix multiplication in terms of Linear Transformations?

  • Let $A$ be an $m \times n$ matrix,
  • then there’s a linear transformation $T_A \ : \ \mathbb R^n \to \mathbb R^m$: $T_A(\mathbf x) = A \mathbf x$ where $A \mathbf x$ is Matrix-Vector Multiplication
  • now let $B$ be an $n \times k$ matrix, then $T_B \ : \ \mathbb R^m \to \mathbb R^k$: $T_B(\mathbf y) = B \mathbf x$
  • what is $T_A \circ T_B$? It’s $T_A \circ T_B \ : \ \mathbb R^k \to \mathbb R^m $
  • $(T_A \circ T_B)(\mathbf x) = T_A \big( T_B(\mathbf x) \big) = T_A \big( B \mathbf x \big) = A \, B \, \mathbf x$
  • $AB$ is matrix-matrix multiplication

Multiplication

We can see matrix by matrix multiplication from 5 different positions:

  • row by column multiplication
  • column at a time
  • row at a time
  • as sum of outer products
  • block multiplication

All of them are equivalent and lead to the same result

Row By Columns

This is usual dot product multiplication:

  • for each row of matrix $A$ we calculate a dot product with each column of matrix $B$
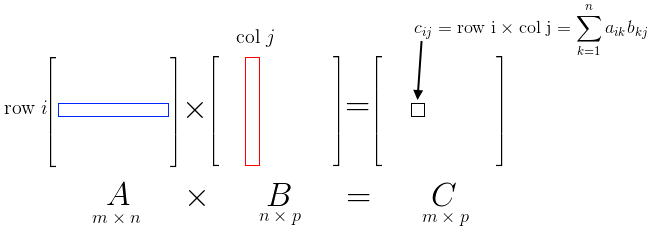
  • Image
  • $c_{ij} = (\text{row $i$ of $A$})^T \times (\text{col $j$ of $B$}) = \sum\limits_{k=1}^{m} c_{ik} b_{kj}$

Column at a Time

For each column $\mathbf{b}_j$ of $B$

  • we multiply each column of $A$ with $\mathbf{b}_j$ - like in column at a time for matrix by vector
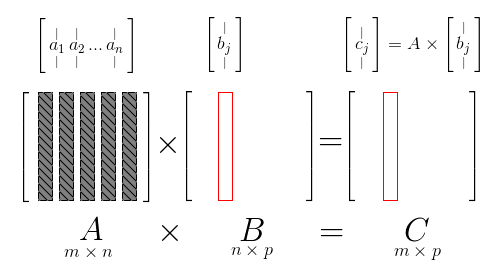
  • Image
  • $\mathbf{c}j = \begin{bmatrix} \mathop{a_1}\limits| ^| \ \mathop{a_2}\limits_|^| \ \cdots \ \mathop{a_n}\limits_|^| |\end{bmatrix} \times \mathbf{b}_j$
  • so each $\mathbf{c}_j$ is a combination of columns of $A$

Row at a Time

For each row $\mathbf{a}^T_i$ of $A$

  • multiply $\mathbf{a}^T_i$ with each rows of $B$ - like for left vector multiplication
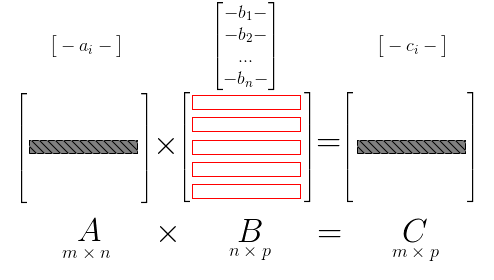
  • Image
  • $\mathbf{c}^T_i = \mathbf{a}^T_i \times B$
  • Note that we can see this as Column at a Time case, but transposed:
    • row at a time in $A\times B = C$ is the same as column at a time in $B^T \times A^T = C^T$

Sum of Outer Products

For $i$ from 1 to $n$,

  • multiply column of $A$ $\mathbf{a}_i$ by row of $B$ $\mathbf{b}^T_i$
  • it gives us a rank-1 matrix - an outer product
  • then sum over all $i$
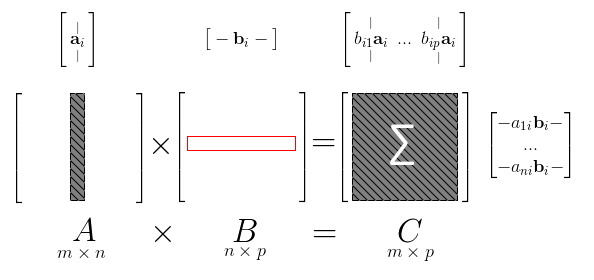
  • Image
  • $C = AB = \sum\limits_{i=1}^n \mathbf{a}_i \mathbf{b}^T_i$

Block Multiplication

$AB = \left[ \begin{array}{c| c} |A_1 & A_2
\hline A_3 & A_4 \end{array} \right] \times \left[ \begin{array}{c| c} |B_1 & B_2
\hline B_3 & B_4 \end{array} \right] = \left[ \begin{array}{c| c} |A_1B_1 + A_2B_3 & A_3B_1 + A_4B_3
\hline A_1B2 + A_2B_1 & A_3B_1 + A_4B_3 \end{array} \right] = C$

Properties

Transposition

  • $(AB)^T = B^T A^T$
  • $(A_1 \cdot \ … \ \cdot A_n)^T = A_n^T \cdot \ … \ \cdot A_1^T$

Inverse Matrices

$(AB)^{-1} = B^{-1} A^{-1}$

  • inverse of product is product of inverses in the reversed order
  • check:
    • $AB \times B^{-1} A^{-1} = A \times (B B^{-1}) \times A^{-1} = A \times I \times A^{-1} A \times A^{-1} = I$
    • $B^{-1} A^{-1} \times AB = B^{-1} \times (A^{-1} A) \times B = B^{-1} \times B = I$

Row Space and Column Space

Let’s show the following:

  • $C(A\, B) \subseteq C(A)$
  • $R(A \, B) \subseteq R(B)$
  • where $C(\cdot)$ is Column Space and $R(\cdot)$ is Row Space

Image of linear transformation

  • first, let’s consider a linear transformation of an $m \times n$ matrix $A$
  • $T_A \ : \ \mathbb R^n \to \mathbb R^m$ : $T_A(\mathbf x) = A \mathbf x$
  • Column Space of $A$ is the image of $T_A$ in $\mathbb R^m$

$C(A\, B) \subseteq C(A)$

  • let $A$ be an $m \times n$ matrix and $B$ be an $k \times n$
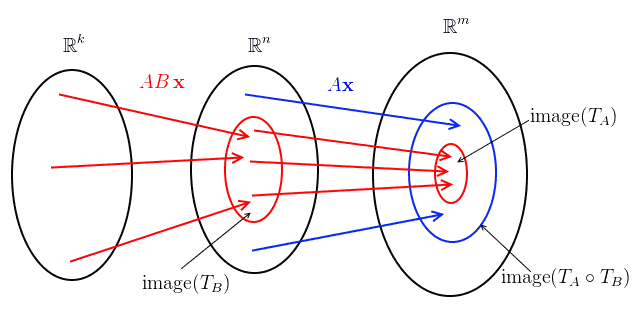
  • $A \, B$ corresponds to linear transformation $T_A \circ T_B$
  • so need to show that $\text{image}(T_A \circ T_B) \subseteq \text{image}(T_A)$
  • Image <| – etc\alg\matrix-mult-image.png –> | | What about $R(A \, B) \subseteq R(B)$?
  • $R(A \, B) = C(B^T A^T) \subseteq C(B^T) = R(B)$

Implementation

SQL

Sparse matrix multiplication

select a.row_num, b.col_num, sum(a.value * b.value)
  from A a, B b
 where a.col_num = b.row_num
group by a.row_num, b.col_num;

MapReduce

  • It’s easy to implement the SQL expression above in terms of MapReduce
  • Link [https://code.google.com/p/stolzen/source/browse/trunk/courses/coursera/Introduction%20to%20Data%20Science/assignment3/p6_matrixmult.py]

E.g. Apache Flink:

text only matrixA.join(matrixB).where(1).equalTo(0) .map(new ProjectJoinResultMapper()).groupBy(0, 1).sum(2)

Full code of Matrix Multiplication in Flink: [https://github.com/alexeygrigorev/aim3/blob/master/src/main/java/de/tuberlin/dima/aim3/assignment3/MatrixMultiplication.java]

Sources

✏️ Edit on GitHub