Preferential Independence
Contents
Preferential Independence
The preference independence principle is an important principle from MCDA for choosing criteria: they should be preferential independent.
Suppose we have 4 alternatives $a,b,c,d$ and a subset of criteria $J \subset G$ such that
- $g_i(a) = g_i(b), \forall i \not \in J$
- $g_i(c) = g_i(d), \forall i \not \in J$
- $g_i(a) = g_i(a), \forall i \in J$
- $g_i(b) = g_i(d), \forall i \in J$
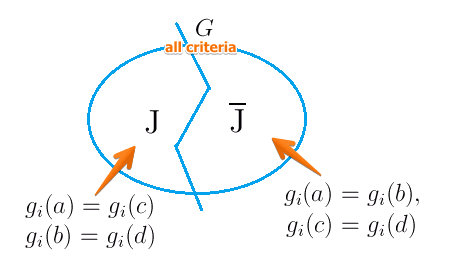
- for criteria that are in $J$, $a$ is the same as $c$ and $b$ is the same as $d$
- for criteria not in $J$, $a$ is the same as $b$, $c$ is the same as $d$
Preferential Independence
- $J \subset A$ is preferentially independent within $G$ when
- if $\forall a,b,c,d \in A$ these conditions hold
- then $a \ P \ b \iff c \ P \ d$
if a decision maker says $a \ P \ b$ we know that he bases his opinion on the set of $J$, because in $\overline{J}$ $a \ I \ b$ - they are the same
Examples
Example 1
| $g_1$ | $g_2$ | $g_3$ | |
|---|---|---|---|
| $a$ | 45 | 70 | 100 |
| $b$ | 50 | 70 | 80 |
| $c$ | 45 | 90 | 100 |
| $d$ | 50 | 90 | 80 |
criteria $\{g_1, g_3\}$ are preferentially independent
- i.e. $a \ P \ b \iff c \ P \ d$
Example 2
In this example the Preferential Independence principle is not satisfied
We're in a restaurant and there are 2 dishes and 2 drinks
- dishes: fish, meat
- drinks: red wine, white wine
- so we have 4 combinations:
| drinks $\downarrow$ | ||
|---|---|---|
| meal $\to$ | $(a)$ fish + white | $(c)$ fish + red |
| $(b)$ meal + white | $(d)$ meal + red | |
So we have two criteria:
- $g_1$ - meal
- $g_2$ - drink
For meal:
- $g_1(a) = g_1(c)$
- $g_1(b) = g_1(d)$
For drink:
- $g_2(a) = g_2(b)$
- $g_2(c) = g_2(d)$
Not satisfied:
- If, when asked "what would you prefer - meat or fish", the decision maker asks "with what drink"
- then the preferential independence is not satisfied: these two criteria are dependent
- usually the case in real life
Satisfied
- if a DM can say
- "I always prefer meat to fish" ($b \ P \ a \land d \ P \ c$) and
- "I always prefer red wine to white wine" ($c \ P \ a \land d \ P \ b$)
- then if he says "I prefer meat with red wine to meat with white line" then he will say "I prefer fish with red wine to fish with white line" ($d \ P \ c \Rightarrow c \ P \ a$)
- usually not the case
Example 3
Taken from [1]
Suppose we are choosing a car and there are two criteria
- style: sport, SUV
- color: red, black
Color is preferentially independent from style when
- if the DM prefers:
- (red, sport) to (black, sport)
- (red, SUV) to (black, SUV)
- then the color is preferentially independent from style
- red is preferred to black regardless of style
-
However style is not necessarily independent from color
- if DM prefers
- (red, sport) to (red, SUV), but
- (black, SUV) to (black, sport)
- then the style is not preferentially independent from color
- because the color influences what decision maker prefers
With graphical depiction it's clear:
-
- red is always preferred to black (all edges come from red to black)
- but when it comes to style, it's not the case: one edge comes from sport to SUV, another from SUV to sport
Example 4
Consider a case when an employer wants to hire a new worker on the basis of their age, degree and professional experience.
| Worker | $g_A$: Age | $g_D$: Degree | $g_E$: Experience |
|---|---|---|---|
| $a$ | 25 | Master | No Experience |
| $b$ | 25 | No Degree | 3 Years |
| $c$ | 35 | Master | No Experience |
| $d$ | 35 | No Degree | 3 Years |
We see that given $J = \{g_A\}$ and $\overline{J} = \{ g_D, g_e \}$:
- $g_i(a) = g_i(b), \forall i \not \in J$
- $g_i(c) = g_i(d), \forall i \not \in J$
- $g_i(a) = g_i(a), \forall i \in J$
- $g_i(b) = g_i(d), \forall i \in J$
However an employee would prefer:
- $a \ P \ b$ but $d \ P \ c$
Preferential Independence in Methods