ML Wiki
Machine Learning Wiki - A collection of ML concepts, algorithms, and resources.

Multi-Criteria Decision Aid

multi-criteria-decision-aid

Multi-Criteria Decision Aid

This is a tool that helps a decision maker to choose a solution when he is facing conflicting criteria and cannot decide.

For example, you want to buy a new car:

  • One is expensive, speed is good;
  • another is cheap but slow and with little comfort.
  • These criteria (cost vs speed) are conflicting.

We need to find a compromise that answers the expectation of a decision maker

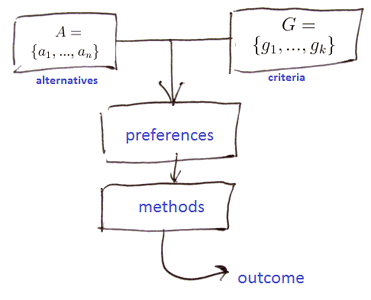
Image

  • Step 1: Define the set of alternatives $A = {a_1, …, a_n}$
  • Step 2: Define the set of criteria $G = {g_1, …, g_k}$
  • Step 3: Define the Preferences (the expectations of a decision maker)
  • Step 4: Apply methods to find the best alternative

Alternatives

$A$ - set of alternatives (actions, options, items, decisions, etc)

$A$ can be

  • finite or infinite
  • countable or uncountable
  • stable (always the same) or evolving

Criteria

A ‘‘criterion’’ $g_i$ is a mapping from the set of alternatives $A$ to some totally ordered set $E_i$:

  • $g_i: A \mapsto E_i$
  • $g_i \in G$ form a set of criteria

With $E_i$ we can rank all elements of $A$ from best to worst

Examples:

  • $E = \mathbb{R}$
  • $E = {\text{VB}, \text{B}, \text{M}, \text{G}, \text{VG}}$

A set can be:

  • ordinal (operations $<, =, >$)
    • $E = {\text{VB}, \text{B}, \text{M}, \text{G}, \text{VG}}$
  • interval (operations $<, =, >, +, -$)
    • temperature
  • ratio (operations $<, =, >, +, -, \cdot, / $)
    • $E = \mathbb{R}$

Restrictions on $G$:

  • For a set to be ordered, operations $<$ and $>$ must be defined there
  • A set of criteria $G$ ideally should form a Consistent Family of Criteria

Dominance Principle

Some alternatives can be eliminated by Dominance principle

  • If for two alternatives $a$ and $b$ for all criteria they are equally good
  • but there exists one criteria at which $a$ is better than $b$
  • then $b$ is dominated by $a$ and will never be chosen

Consider this example

  • we’re choosing a car
  • there are 4 criteria: price, power, consumption, comfort
  • there are 6 alternatives
  Price Power Consumption Comfort Avg A. 18 75 8 3   Sport 18.5 110 9 2   Avg B. 17.5 85 7 3   Lux 1 24 90 8.5 5   Exonomic 12.5 50 7.5 1   Lux 2 22.5 85 9 4

By Dominance principle:

  • We see that ‘'’Avg B’’’ is always better than ‘'’Avg. A’’’
  • then nobody will ever choose Avg A: A is dominated by B
  • but no other alternative can be eliminated this way

How to chose which one is the best?

  • Need ‘‘subjective’’ preferences

Preferences

To be able to find the best solution we need to know ‘‘subjective preferences’’

Given two alternatives $a$ and $b$ a decision maker can say if

  • $a \ P \ b$ or $b \ P \ a$: $a$ is preferred to $b$ - ‘‘the preference relation’’
  • $a \ I \ b$ - the indifference relation (not transitive see Luce’s Coffee Cups) - $a \ J \ b$ - the incomparability relation, when you cannot compare things

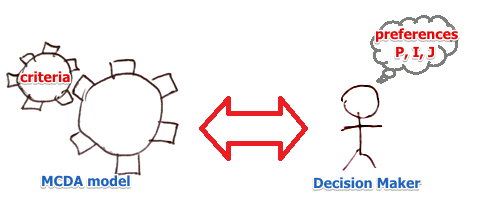
Image

How to represent a Decision Maker’s preferences in some model?

With Modeling Preferences:

Important condition when modeling preferences:

Methods

There some important families of criteria:

Outranking

Outranking methods perform pair-wise comparisons (like in the Condorcet’s Rule)

Most famous methods:

Problems of outranking methods:

Multi-Objective Optimization

Once we found the Pareto-optimal set of solutions in a problem, we need to find the best solution, and MCDA can help with it

  • http://www.lamsade.dauphine.fr/~bouyssou/TranspaOrbel16.pdf
  • http://www.liacs.nl/~emmerich/moda03mcda.pdf

Sources

✏️ Edit on GitHub