Partial Order
This is a preference structure for Modeling Preferences in MCDA that includes $J$ - the Incomparability relation.
Assume:
- there are different experts ${1, 2, 3}$
- they evaluate 4 projects $a, b, c, d$
- investment $a$ is preferred to investment $b$ if estimates from $a$ are higher than from $b$ (or $a$ dominates $b$)
- i.e. there is Unanimity between the experts
| | $a$ | $b$ | $c$ | $d$ | 1 | 10 | 8 | 7 | 6 || 2 | 9 | 7 | 5 | 6 || 3 | 12 | 8 | 9 | 4 | We can infer the following relations:
- $a \ P \ b$ because all three experts agree
- but $b \ J \ c$:
- 1st expert say $b \ P \ c$
- but 3rd say $c \ P \ b$
- therefore we cannot compare $a$ and $b$
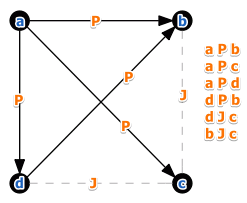
so we have partial order:
- $P$ is transitive
- and $J$ is not empty