Query Result Size Estimation
Choosing a physical operator for a Relational Algebra operator depends on
- a particular case and statistics kept in Database System Catalog
- note that this data is kept only for base relations, not for sub-results
- but we need to be able to estimate them for sub-results as well| | |
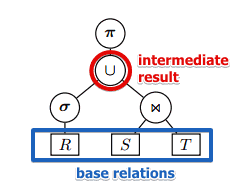
- but we need to be able to estimate them for sub-results as well| | |
- note that these measures depend only on
- statistics
- and Logical Query Plan and not on Physical Query Plan (no matter what physical algorithm we apply we will end with exactly same result)
So the goal:
- for every internal node $n$ estimate parameters
- $B(n)$ - the number of blocks,
- $T(n)$ - the number of tuples,
- $V(n, A_1, …, A_k)$ - the number of distinct values
- note that we can compute $B(n)$ given (1) $T(n)$ (2) size of each tuple in $n$ and (3) size of a block
Projection
for ‘‘bag-based’’ projection $\pi_L (R)$ the general formula is
- $T(\pi_L (R)) = T(R)$: tuples are not eliminated
- but $B(\pi_L (R))$ can change since the size of each tuple changes
Example
Relation $R(A, B, C)$
- $A, B$ - 4 bytes int, $C$ - 100 bytes string
- each tuple has header 12 bytes
- block size: 1024 bytes, and block header is 24 bytes
- $T(R) = 10000, B(R) = 1250$
- how many blocks needed to store $\pi_{A,B}(R)$
Solution
- 1024 - 24 = 1000 bytes per block
- 12 + 4 + 4 = 20 bytes per projected record
- 1000 / 20 = 50 tuples per block
- $B(\pi_{A,B}(R)) = T(\pi_{A,B}(R)) / 50 = 10000 / 50 = 200$
If size of records is variable, it’s harder.
- In this case usually keep some statistics to estimate the avg size of a projected record
Selection
$\sigma_p(R)$ for some filtering predicate $p$
- estimation is $T(\sigma_p(R)) = T(R) \times \text{sel}_p (R)$
- where $\text{sel}_p (R)$ is selectivity of predicate $p$ on relation $R$
- or the probability that a tuple $t \in R$ will satisfy $p$
- calculating $\text{sel}_p$ depends on the type of predicate $p$
Equality
Selection $\sigma_{A = c}(R)$ where $c$ is a constant
- $\text{sel}_{A = c} (R) = \cfrac{1}{V(R, A)}$
- where $V(R, A)$ is the number of distinct values in $R$
- in this case for simplicity we assume the uniform distribution of values in $R$
Example
- Given: $R(A, B, C)$, $T(R) = 10000$, $V(R, A) = 50$
- $T(\sigma_{A = 10}(R)) = \cfrac{T(R)}{V(R, A)} = \cfrac{10000}{50} = 200$
But typically Databases collect some statistics in the Database System Catalog
| range | [1, 10) | [11, 20) | [21, 30) | [31, 40) | [41, 50) || # of tuples | 50 | 2000 | 2000 | 3000 | 2950 |
- suppose we have equal-width histogram on $A$:
- then we can estimate $\text{sel}{A = 10} = \underbrace{\cfrac{50}{10000}}{50 values} \times \underbrace{\cfrac{1}{10}}_{10 possible values}$
Inequality
Selection $\sigma_{A < c} (R)$ where $c$ is constant
Suppose we don’t have any statistics
- in this case we apply a simple following heuristic
- $\text{sel}{A < c} = \cfrac{1}{2} or \text{sel}{A < c}(R) = \cfrac{1}{3}$
- rationale: queries with inequalities usually retrieve a small fraction of the possible tuples, not all of them
Example
- Given: $R(A, B, C), T(R) = 10 000$
- estimation: $T(\sigma_{B < 100} (R)) = T(R) / 3 = 3334$
Better estimates are possible if we have some statistics
- Given: $R(A, B, C), T(R) = 10 000$, values of $B$ lay in range [8, 57] distributed uniformly
- Therefore $V(R, B) \leqslant 57 - 8 + 1$ - that many values of $B$ are possible
- Estimate $\text{sel}_{B < 10} (R)$
- only $B = 8$ and $B = 9$ satisfy $B < 10$
- therefore $\text{sel}_{B < 10} (R) = \cfrac{2}{50} = 0.04$
- and $T(\sigma_{B < 10} (R)) = T(R) \times 0.04 = 400$
Inequality
Selection $\sigma_{A \ne c} (R)$ where $c$ is constant
- this is the inverse of $\sigma_{A = c} (R)$
- $\text{sel}_{A \ne c} (R) = \cfrac{V(R, A) - 1}{V(R, A)}$
- this is estimated probability that a tuple doesn’t satisfy the predicate $A = c$
Inversion (Not)
Selection $\sigma_{\text{not}(p)} (R) $
- same as for Inequality
- $\text{sel}{\text{not}(p)} (R) = 1 - \text{sel}{p} (R)$
And
Selection $\sigma_{p_1 \land p_2} (R)$
- $\sigma_{p_1 \land p_2} (R) = \sigma_{p_1} \sigma_{p_2} (R) = \sigma_{p_2} \sigma_{p_1} (R)$ (order doesn’t matter)
- in this case, $\text{sel}{p_1 \land p_2}(R) = \text{sel}{p_1}(R) \times \text{sel}_{p_2}(R)$
- important assumption: $p_1$ and $p_2$ are independent
- for example, doesn’t hold for $A > 100 \land A < 200$ - because the conditions are correlated in this case
Example
- $T(R) = 10000, V(R, A)$ = 50
- estimate $T(\sigma_{A = 10 \land B < 10 (R)})$:
- $T(R) \times \text{sel}{A = 10} (R) \times \text{sel}{B < 10} (R) = \cfrac{T(R)}{V(R, A) \times 3} = 67$
Or
Selection $\sigma_{p_1 \lor p_2} (R)$
- $\text{sel}{p_1 \lor p_2} (R) = \min (\text{sel}{p_1} (R) + \text{sel}_{p_2} (R), 1)$
- it cannot be greater than 1
- assumptions
- $p_1$ and $p_2$ are independent
- also they select disjoint sets of tuples (otherwise we would count some tuples twice)
Another way: to use De-Morgan Rule
- $p_1 \lor p_2 \equiv \overline{\overline{p_1} \land \overline{p_2}}$ (the line over means ‘'’not’’’)
- $\text{sel}{p_1 \lor p_2}(R) = 1 - (1 - \text{sel}{p_1}(R)) \times (1 - \text{sel}_{p_2}(R))$
- in this case we also have the same assumptions
Cartesian Product
$R \times S$
The general formula is:
- $T(R \times S) = T(R) \times T(S)$
Joins
Simple Cases
$R \Join S, R(X, Y), S(Y, Z)$ (i.e. we join on $Y$)
- $R$ and $S$ have no tuples in common
- $T(R \Join S) = 0$
- $Y$ is a key in $S$ and a foreign key of $R$
- each tuple of $R$ joins exactly with one tuple in $S$
- $T(R \Join S) = T(R)$
- almost all tuples of $R$ and $S$ have the same $Y$ value
- then $T(R \Join S) \approx T(R) \times T(S)$ (degenerates to a Cartesian product)
One Join Attribute
$R \Join S, R(X, Y), S(Y, Z)$ (i.e. we join on $Y$)
- it’s same as selection with predicate $R.Y = S.Y$
Simplifications
For other harder cases we need the following simplifications:
’'’Containment’’’ of Value Sets
- if $R(V, Y) \leqslant V(S, Y)$
- then every value of $Y \in R$ will have a joining tuple with $Y \in S$
- that means: all matched values in $X$ will have a corresponding value in $Y$ - or vice-versa
’'’Preservation’’’ of Value Sets
- when joining two relations, all non-matching attributes are not lost
- i.e. they get transfered to the results
- (if we join two relations on $Y$, $R$ has $X$ and $S$ has $Z$, then all possible values are going to occur in the output)
- i.e. $V(R \Join S, X) = V(R, X)$ and $V(R \Join S, Z) = V(S, Z)$
Under there simplification we will consider two cases
Case 1
$V(R, Y) \leqslant V(S, Y)$ (say one-to-many relationship)
- every tuple if $R$ has a match is $S$ by the containment assumption
- or each tuple in $R$ has $\approx \cfrac{T(S)}{V(S, Y)}$ tuples in $S$ (assuming uniform distribution)
- therefore $T(R \Join S) = T(R) \times \cfrac{T(S)}{V(S, Y)}$
Case 2
$V(R, Y) \geqslant V(S, Y)$ (say many-to-one relationship)
- each tuple in $S$ has $\approx \cfrac{T(R)}{V(R, Y)}$ tuples in $R$
- therefore $T(R \Join S) = T(S) \times \cfrac{T(R)}{V(R, Y)}$
General Case
$T(R \Join S) = \cfrac{T(S) \times T(R)}{\min(V(R, Y), V(S, Y))}$
More Join Attributes
Now assume that we join on two attributes $Y_1, Y_2$:
- $R(X, Y_1, Y_2) \Join S(Y_1, Y_2, Z)$
- (under the same assumptions)
- same as selection with predicate with AND: $R.Y_1 = S.Y_1 \land R.Y_2 = S.Y_2$
Case 1
$V(R, Y_1) \leqslant V(S, Y_1)$ and $V(R, Y_2) \leqslant V(S, Y_2)$
- a tuple in $R$ has $\cfrac{1}{V(S, Y_1)} \times \cfrac{1}{V(S, Y_2)}$ chance of joining with a tuple in $S$
- (again assuming uniform distribution)
- therefore $T(R \Join S) = T(R) \times \cfrac{T(S)}{V(S, Y_1) \times V(S, Y_2)}$
Case 2
$V(S, Y_1) \leqslant V(R, Y_1)$ and $V(S, Y_2) \leqslant V(R, Y_2)$
- symmetric to Case 1
- chance of tuple from $S$ joining with $R$ is $\cfrac{1}{V(R, Y_1)} \times \cfrac{1}{V(R, Y_2)}$
- therefore $T(R \Join S) = T(S) \times \cfrac{T(R)}{V(R, Y_1) \times V(R, Y_2)}$
Case 3
$V(R, Y_1) \leqslant V(S, Y_1)$ but $V(S, Y_2) \leqslant V(R, Y_2)$
- chance of tuple from $R$ joining with $S$ is $\cfrac{1}{V(R, Y_1)} \times \cfrac{1}{V({\color{blue}{S}}, Y_2)}$
- therefore $T(R \Join S) = T(R) \times \cfrac{T(S)}{V(R, Y_1) \times V(S, Y_2)}$
Case 4
$V(S, Y_1) \leqslant V(R, Y_1)$ but $V(R, Y_2) \leqslant V(S, Y_2)$
- chance of tuple from $R$ joining with $S$ is $\cfrac{1}{V({\color{blue}{S}}, Y_1)} \times \cfrac{1}{V(R, Y_2)}$
- therefore $T(R \Join S) = T(R) \times \cfrac{T(S)}{V(S, Y_1) \times V(R, Y_2)}$
General Formula
$T(R \Join S) = \cfrac{T(R) \times T(S)}{\max(V(R, Y_1), V(S, Y_1) \times \max(V(R, Y_2), V(S, Y_2)}$
This formula generalizes to more than 2 joining attributes