ML Wiki
Machine Learning Wiki - A collection of ML concepts, algorithms, and resources.

Rule-Based Classifier

classifiers machine-learning

Rule-Based Classifier

Rule-based classifiers

  • use a set of IF-THEN rules for classification
  • if {condition} then {conclusion}
  • if part - ‘‘condition’’ stated over the data
  • then part - a class label, ‘‘consequent’’

1-Rule

Example

Suppose we have the following dataset | + Titanic dataset [http://www.kaggle.com/c/titanic-gettingStarted/data] || pclass | sex | age | sibsp | parch | fare | embarked | survived | 3 | male | 22 | 1 | 0 | 7.25 | S | 0 || 1 | female | 38 | 1 | 0 | 71.28 | C | 1 || 3 | female | 26 | 0 | 0 | 7.93 | S | 1 || 1 | female | 35 | 1 | 0 | 53.10 | S | 1 || 3 | male | 35 | 0 | 0 | 8.05 | S | 0 || 3 | male | | 0 | 0 | 8.46 | Q | 0 || 1 | male | 54 | 0 | 0 | 51.86 | S | 0 || 3 | male | 2 | 3 | 1 | 21.08 | S | 0 || 3 | female | 27 | 0 | 2 | 11.13 | S | 1 || 2 | female | 14 | 1 | 0 | 30.07 | C | 1 || 3 | female | 4 | 1 | 1 | 16.70 | S | 1 || 1 | female | 58 | 0 | 0 | 26.55 | S | 1 | If we visualize the data by sex

  • color-coding survived with blue and not survived with red
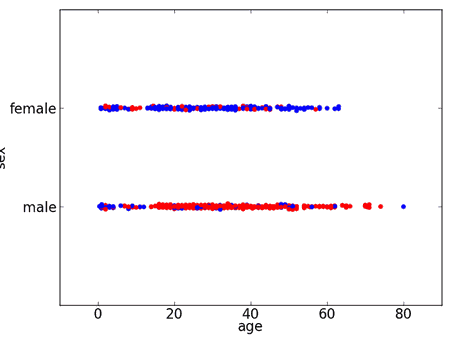
  • Image
  • so we see that most women survived $\to$ can assume that all survived
  • e.g. have a rule $x.\text{women} \Rightarrow \text{survived}$

Rules

  • there could be many rules like this
  • if most children under 4 survived, assume all children under 4 survived
  • if most people with 1 sibling survived, assume all people with 1 sibling survided
  • calculate misclassification error (error rate) and take the best| | | Some variables have more than 2 values
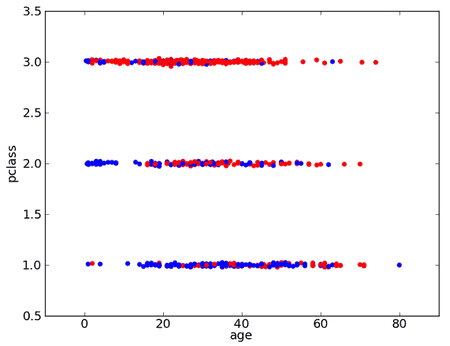
  • Image
  • if pclass = 1 then survived=yes
  • if pclass = 2 then survived=yes
  • if pclass = 3 then survived=no

One Rule Algorithm

  • for each attribute $A$
  • for each value $V$ of $\text{dom}(A)$
  • create a rule
    • find the most frequent class $c$
    • create a rule “if $A = V$ then $c$
    • calculate the error rate of this rule
  • select attribute with best error rate for its rules

Can see 1-Rule as a one-level Decision Tree (Data Mining)

  • one branch for each value
  • each branch assigns most frequent class

Several Conditions

We also can consider several attributes at the same time

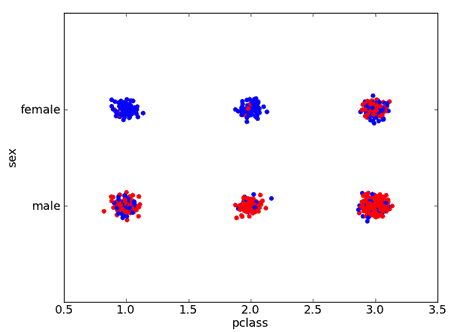
  • Image
  • IF pclass=’1’ AND sex=’female’ THEN survive=yes
  • IF pclass=’2’ AND sex=’female’ THEN survive=yes
  • IF pclass=’2’ AND sex=’male’ THEN survive=no
  • IF pclass=’3’ AND sex=’male’ THEN survive=no
  • …

Can go further

  • IF pclass=’3’ AND sex=’female’ AND age < 4 THEN survive=yes
  • IF pclass=’3’ AND sex=’female’ AND age >= 4 THEN survive=no
  • IF pclass=’1’ AND sex=’male’ AND age < 5 THEN survive=yes

Getting Rules

Where to extract these rules from?

  • from Decision Trees
    • each path from top to the bottom is a rule, and the leaf is a class
  • sequential covering - for learning rules directly (PRISM algorithm [http://www.cs.bc.edu/~alvarez/DataMining/Notes/covering.html])
    • repeatedly removes a portion of the dataset
    • the portion - instances covered by the most promising rule at each stage

Sequential Covering Algorithm

’'’PRISM’’‘(dataset $D$):

  • $R$ - resulting rule dataset, $R \leftarrow \varnothing$
  • for each class $C$
  • while $D \not \equiv \varnothing$
    • $r \leftarrow$ FindNextRule($C, D$)
    • $R \leftarrow R \cup { r }$
    • remove from $D$ all instances correctly classified by $r$

Finding the next rule [http://www.evernote.com/shard/s344/sh/d82d9776-7319-4ce2-8cb3-f96c59dd70ba/86a3d6d63dc9ffef6e0420cd0944e845]

  • FindNextRule($C, D$) subroutine
  • uses Depth-First Search to construct the next rule for class $C$
  • we know the consequent for this rule: it’s $C$
  • so we need to construct only ‘‘antecedent’’ (предыдущий член отношения)
    • start with an empty antecedent,
    • iteratively add most promising “attribute=value” constraints
    • use error rate to get the best one
  • continue DFS until the rule is specific enough to make no classification errors in the given dataset

’'’FindNextRule’’‘(class $C$, dataset $D$):

  • let $A$ be all attributes in $D$
  • let $r$ be the initial rule $r: \varnothing \to C$
    • not examining anything, just always returning $C$
  • while $r$ incorrectly classifies some non-$C$ instances in $D$
    • let $\text{ant}(r) \to C$ be the rule computed at the previous iteration
      • $\text{ant}(r)$ is the ‘‘antecedent’’ of $r$;
      • it means take the rule from the previous iteration of the rule creation loop
      • (or an empty rule if this is the first iteration)
    • for each pair $(a, v)$ s.t. $a \in A$ and $v \in \text{dom}(a)$
      • consider rule $\text{ant}(r) \land (a = v) \to C$
      • calculate the accuracy of this rule
    • let $(a^, v^)$ be the pair with the best accuracy
    • so update $r$ by adding this condition:
      • let $r: \text{ant}(r) \land (a^* = v^*) \to C$
    • remove attribute $a^*$ from $A$:
      • $A \leftarrow A - { a^* }$
  • return $r$

Example

A good example of PRISM can be found at [http://www.cs.bc.edu/~alvarez/DataMining/Notes/covering.html]

Strategies for Learning Rules

General-to-Specific

  • start with an empty rule
  • add constraints to eliminate negative examples
  • stop when only positive examples are covered

Specific-to-General

  • start with a rule that identifies a single random instance
  • remove constraints to cover more positive examples
  • stop when further generalization starts covering negatives

Evaluation

Each rule can be evaluated using these measures

  • coverage: # of data points that satisfy conditions
  • accuracy = # of correct predictions / coverage

Other measures of “promisingness”

  • Information Gain
  • see page 38 at [http://www.slideshare.net/pierluca.lanzi/machine-learning-and-data-mining-12-classification-rules]
  • Introduction to Data Science (coursera)
  • http://www.slideshare.net/pierluca.lanzi/machine-learning-and-data-mining-12-classification-rules
  • http://www.tutorialspoint.com/data_mining/dm_rbc.htm
  • http://www.cs.bc.edu/~alvarez/DataMining/Notes/covering.html
✏️ Edit on GitHub