Workflow Soundness
Soundness is a notion of correctness of workflow nets
- for Petri Nets and Workflow Nets
- for YAWL
These properties are usually checked with Reachability Graphs
Situations to Avoid
Unboundness
'’Unboundness’’ means:
- there is no bound on the number of tokens that a place can hold
- this always means a problem
Improper Termination
A workflow net satisfies ‘‘proper completion’’ when
- if there’s a token in the output place, then there are no tokens in other places
- if this property is not satisfied, then the problem is called ‘‘improper termination’’
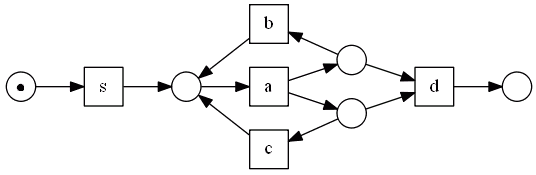
- firing sequences:
- $s \to a \to b \to a \to d$
- $s \to a \to c \to a \to d$
- there are remaining tokens after the flow ends
- it means: it stopped, but there is still some work to do
- clearly it’s a problem
Example:
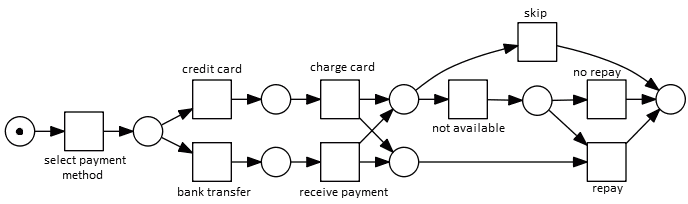
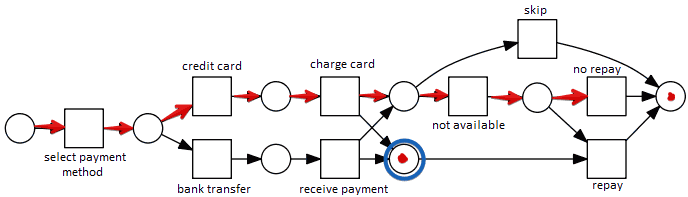
- there are paths that lead to proper termination:
- card $\to$ charge $\to$ skip $\to$ finish
- transfer $\to$ receive payment $\to$ NA $\to$ repay
- but there are problematic firing sequences
- card $\to$ charge $\to$ NA $\to$ no repay $\to$ finish
- at the step of no-repay both repay and no repay are available
- after firing no repay there’s one token left in the network
Deadlocks and Livelocks
Both livelock and deadlock mean that
- there’s a situation when you cannot reach the end
Deadlock
- once you fire $a$ nothing is enabled
- but the workflow in not complete: there’s no token in the output place
- in this case we don’t have matching joins - that leads to a deadlock
Livelock
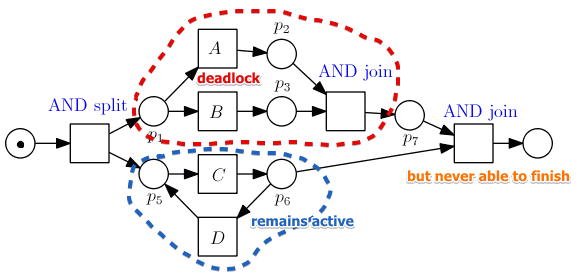
- $C$ and $D$ can fire forever: they’re always enabled
- but the workflow will never reach the end
Dead Transitions
A dead transition
- is a transition that can never fire
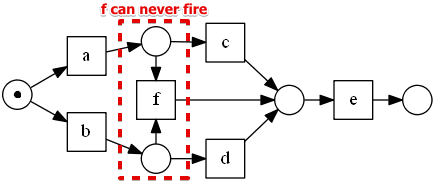
- in this case $F$ never gets activated
- this workflow can finish successfully
- the only fix - to remove the dead transition
Petri Nets
For Petri Nets that represent infinite processes there is a notion of correctness of there nets:
- liveness
- boundness
- deadlock-free
Used notation:
Liveness
In a ‘‘live’’ petri net there are no dead transitions
- a dead transition is a transition that can never fire in any marking reachable from the initial marking
a petri net $N$ with initial marking $M_0$ is live $\iff$
- $\forall M: M_0 \to^* M, \forall t: \exists M \to^* M’$ in which $t$ is enabled
It reads:
- for any marking $M$ reachable from the initial marking $M_0$
- and for every transition $t \in T$
- there exists a marking $M’$ reachable from $M$ s.t.
- $t$ is enabled in $M’$
In other words:
- no matter what happens, for any $t$ there exists a marking $M’$ reachable from the current state $M$
- such that $t$ is enabled in it
Example
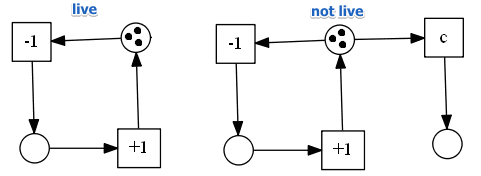
- the example on the left is live: no matter what happens the process continues
- the net on the right is not live: after firing $ccc$ nothing is active anymore
Example 2
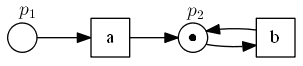
- this network is deadlock-free
- Reachability Graph:
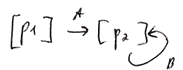
- so whatever we do there are always active transitions
- but we cannot escape marking $[p_2]$, and $a$ is no longer live
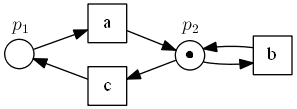
- but if we add another transition $c$ it becomes live:
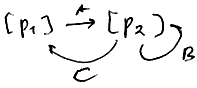
So liveness means:
- no matter what happens, every transition $t$ should be able to fire at some point in future
Boundness
A petri net $N$ with initial marking $M_0$ is $k$-‘‘bounded’’ iff
- $\forall M: M_0 \to^* M, \forall p \in P: M(p) \leqslant k$
- there never can appear more than $k$ tokens in any $p \in P$ in any reachable marking $M$
5-bounded net:
- each $p$ can hold no more than 5 tokens
1-bounded net is called ‘‘safe’’
Example

- in this net $a$ can fire infinitely many number of times
- so this net is not bounded
- but it’s always live: there exists matchings for which $a$ and $b$ can fire
Example 2
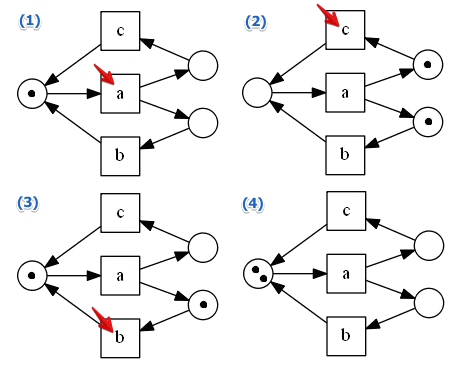
- not bounded: can put as many matchings as we want
Deadlock Free
a petri net $N$ with initial marking $M_0$ is ‘‘deadlock-free’’ iff
- $\forall M: M_0 \to^* M \ \exists M’: M \to M’$
- for any reachable marking $M$ there exists another marking $M’$ that can be reached from $M$
- i.e. every reachable marking enables some transition $t \in T$
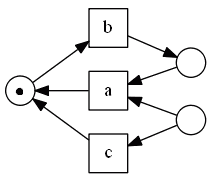
- after $b$ fires nothing can fire anymore
- $a$ needs tokens from two its input places, but there’s only one token
Workflow Nets Soundness
With workflow nets
- we can decide many things statically, before enacting the workflow
- there are some desirable properties that help to avoid these problems
A ‘‘workflow net’’ is sound $\iff$ it has
- the option to complete
- proper completion
- no dead transitions
Notation:
- $M_0 = [i]$ initial marking
- $[o]$ - final marking
- also notation from Petri Nets and Reachability Graph
- given a petri net $N = (P, T, F)$
Option to Complete
$\forall M, M_0 \to^* M: \exists M’, M \to^* M’: M’ \geqslant [o]$
- for all $M$ reachable from the initial marking
- it should be possible to reach the final marking from $M$
Example:
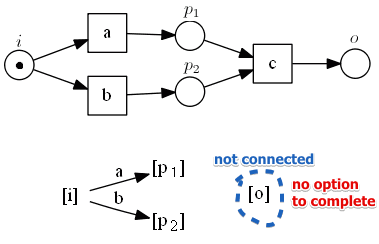
- deadlock = no option to complete
- marking $[o]$ is not reachable from $[i]$
Livelock Example:
- consider the net with a livelock
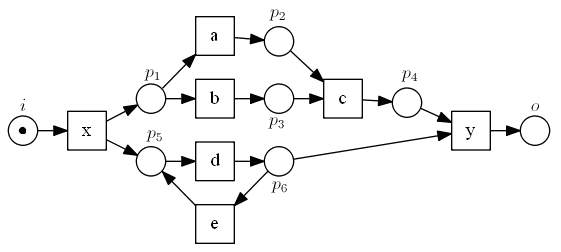
- the following is its reachability graph
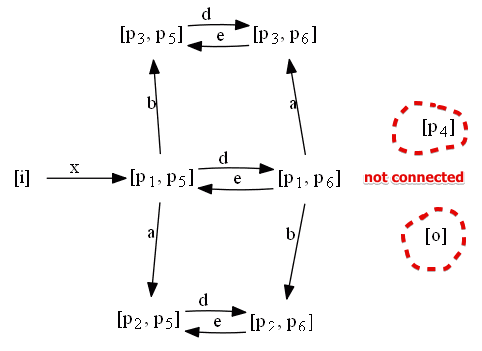
- we see that two nodes are not connected: it’s clearly a problem
Proper Completion
$M_0 \to ^* M \land M \geqslant [o] \Rightarrow M \equiv [o]$
- when $M$ is reachable from the initial marking
- and it’s great or equal to the final marking
- for proper completion to hold $M$ should be equal to $[o]$
No Dead Transitions
$\forall t \in T, \exists M: M_0 \to^* M$ and $t$ in enabled in $M$
- for all possible transitions there should exists at least one marking $M$ in which $t$ is enabled
Petri Net Soundness
A sound workflow net can never be live:
- it should be able to reach the final state
- and nothing should be able to fire from that state
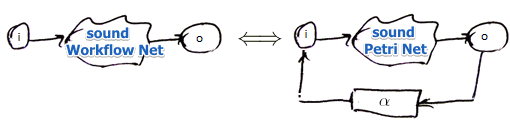
A workflow net $N = (P, T, F)$ is sound iff
- a petri net $N’ = (P, T \cup { \alpha }, F \cup { (o, \alpha), (\alpha, i) } )$ is sound
So we just connect $o$ and $i$ via some transition $\alpha$
- and check Petri Net soundness
Relation:
- if $N$ doesn’t have the proper completion property, $N’$ will not be bounded
- if there’s a deadlock in $N$,
- there exists a firing sequence in $N’$ s.t.
- it brings you to some state where you cannot reach $o$
- i.e. $N’$ is not live
- dead transitions: same notion in both $N$ and $N’$