Contents
Cumulative Gain Chart
Gain Charts are used for Evaluation of Binary Classifiers
- also it can be used for comparing two or more binary classifiers
- the chart shows $\text{tpr}$ vs $\text{sup}$
Motivating Example
Suppose we have a direct marketing campaign
- population is very big
- we want to select only a fraction of the population for marketing - those that are likely to respond
- we build a model that scores receivers - assigns probability that he will reply
- want to evaluate the performance of this model
Cumulative Gain
Performance evaluation
- recall values that can be calculated for Evaluation of Binary Classifiers
- accuracy - but it's not enough here
- $\text{tpr}$ - True Positive Rate or Sensitivity
- $\text{tpr} = \cfrac{\text{TP}}{\text{TP} + \text{FN}}$
- fraction of examples correctly classified
- $\text{sup}$ - Support (Predictive Positive Rate)
- $\text{sup} = \cfrac{\text{TP} + \text{FP}}{N} = \cfrac{\text{predicted pos}}{\text{total}}$
- fraction of positively predicted examples
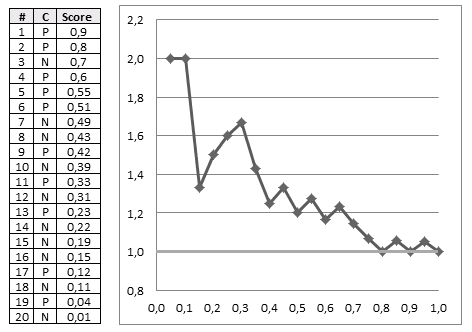
Suppose that we obtained the following data:
- Cls = actual class
- score = predicted score
|
$\Rightarrow$ sort $\Rightarrow$ |
|
|
Intuition
- suppose now we select top 20% records
- we see that out of 4 examples 3 of them are positive
- in total, there are 10 responders (positive classes)
- so with only 20% (4 records) we can target 3/10 = 30% responders
- we also can use a random model
- if you randomly sample 20% of records, you can expect to target only 20% your responders
- 20% of 10 = 2
- so we're doing better than random
- can do it for all possible fractions of our data set and get this chart:
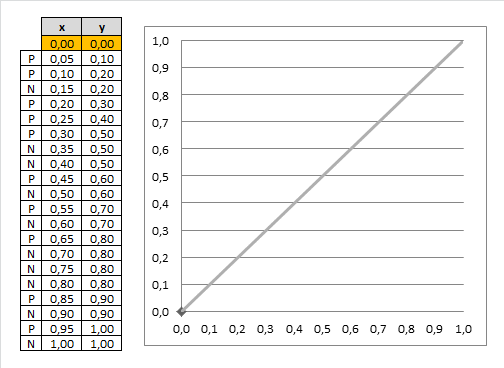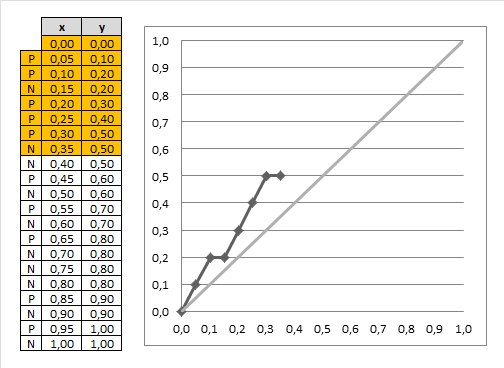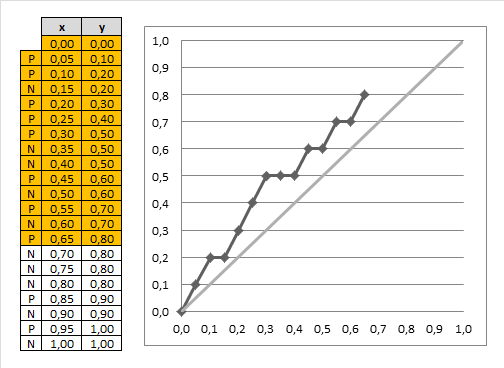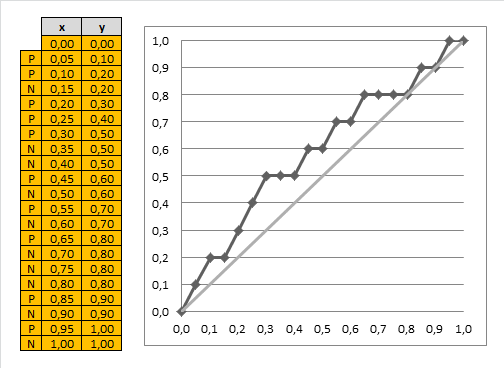
Best classifier
- the optimal classifier will score positives and negatives s.t. there's a clear separation between them
- in such a case the gain chart will always go up until it reaches 1, and then go left
-
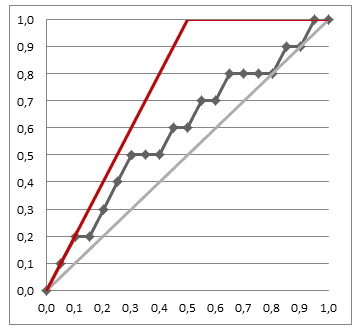
- the closer our chart to the best one, the better our classifier is
Gain Chart
So a gain chart shows
- Predicted Positive Rate (or support of the classifier)
- vs True Positive Rate (or sensitivity of the classifier)
-
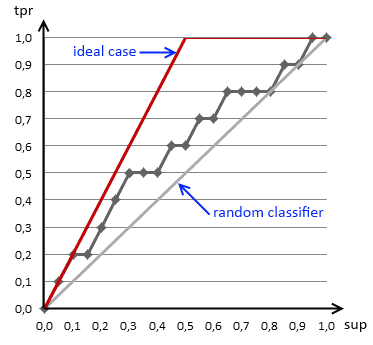
- it says how much population we should sample to get the desired sensitivity of our classifier
- i.e. if we want to direct 40% of potential repliers to our targeting campaign, we should select 20%
- when we divide our data into two subsets, we can plot the charts for both
-

- we can easily see if a classifier overfits on the test set, but underperforms on the testing
Examples
Given
- 20 training examples, 12 negative and 8 positive
|
$\Rightarrow$ sort(score) |
|
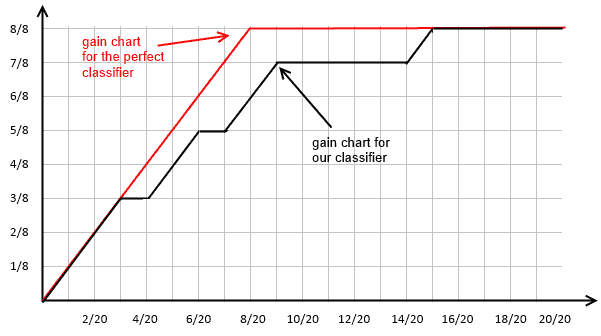
Comparing Binary Classifiers
Can draw two or more gain charts over the same plot
- and thus be able to compare two or more classifiers
-
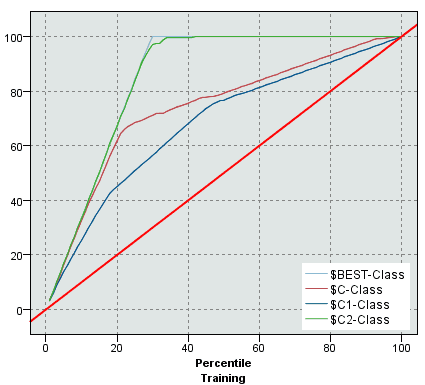
- we see that one of the classifiers most likely overfits the training data
-
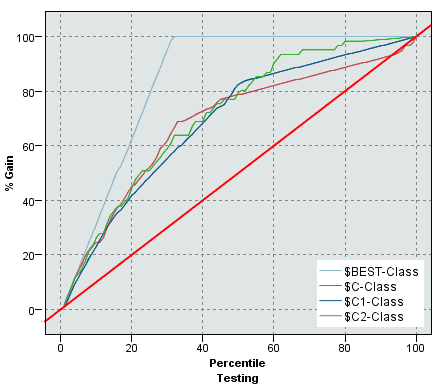
- but when we test, we see that it performs as good (bas) as other classfiers
Plotting Gain Chart in R
In R there's a package called ROCR [1] (for drawing ROC Curves)
install.packages('ROCR')
require('ROCR')
It can be used for drawing gain charts as well:
cls = c('P', 'P', 'N', 'P', 'P', 'P', 'N', 'N', 'P', 'N', 'P',
'N', 'P', 'N', 'N', 'N', 'P', 'N', 'P', 'N')
score = c(0.9, 0.8, 0.7, 0.6, 0.55, 0.51, 0.49, 0.43,
0.42, 0.39, 0.33, 0.31, 0.23, 0.22, 0.19,
0.15, 0.12, 0.11, 0.04, 0.01)
pred = prediction(score, cls)
gain = performance(pred, "tpr", "rpp")
plot(gain, col="orange", lwd=2)
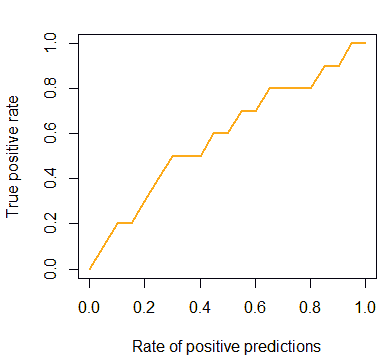
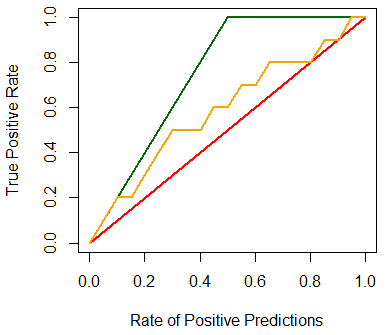
But we also can add the baseline and the ideal line:
plot(x=c(0, 1), y=c(0, 1), type="l", col="red", lwd=2,
ylab="True Positive Rate",
xlab="Rate of Positive Predictions")
lines(x=c(0, 0.5, 1), y=c(0, 1, 1), col="darkgreen", lwd=2)
gain.x = unlist(slot(gain, 'x.values'))
gain.y = unlist(slot(gain, 'y.values'))
lines(x=gain.x, y=gain.y, col="orange", lwd=2)
Cumulative Lift Chart
Lift charts show basically the same information as Gain charts
- $\text{ppr}$ Predicted Positive Rate (or support of the classifier)
- vs $\cfrac{\text{tpr}}{\text{ppr}}$ True Positive over Predicted Positive
-