Alpha Algorithm
$\alpha$ algorithm one of the first Process Mining algorithm that discovers Workflow Nets (in form of Petri Nets) from logs
The process of (re-)discovering a workflow consists of 3 phases:
- pre-processing
- inferring relations between the transitions
- processing
- execution of the alpha algorithm
- post-processing
Definitions
Implicit Places
One important caveat: implicit places. A place is ‘‘implicit’’ if adding or removing it does not cause the behavior of a workflow.
Example
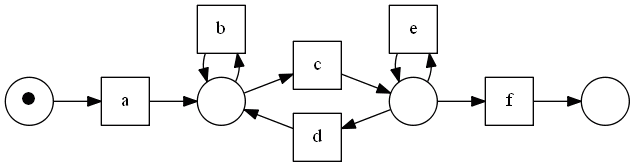
- This workflow does not contain any implicit places
- :
- but if we connect $a$ and $d$ with a new place - this place will be implicit
- :
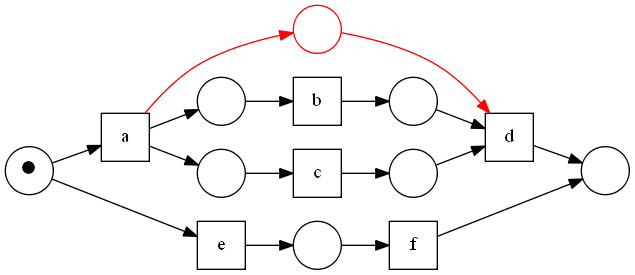
These places cannot be seen from the logs since they have no affect on the behavior
- typically mining algorithm cannot find such places
Complete Log
We assume that the log we feed into this algorithm is complete.
A log of a workflow net $N$ is ‘‘complete’’ if
- if it contains all other possible logs of $N$
- it contains all transitions $t$ from this $N$
For example,

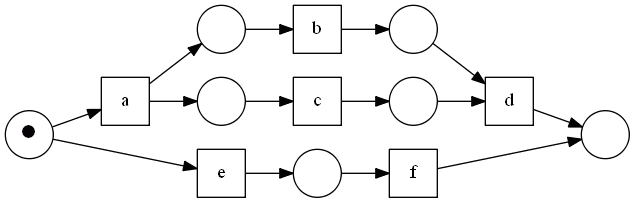
- for this workflow the complete log is $[abcd, acbd, ef]$ - it covers all possible traces
The Alpha Algorithm
Relations
In order to find discover a workflow net from logs, we need to establish the ordering between the transitions of this workflow. These relations will later be used in order to find places and connection between the transitions and these places.
We define the following relations between transitions in the log
- '’direct succession’’ $x > y$
- $x > y \iff$ we see in log sub-traces $…xy…$
- '’causality’’ $x \to y$
- $x \to y \iff x > y \land y \not > x$
- i.e. if there are traces $…xy…$ and no traces $…yx…$
- this relation may mean that we will need to put a place between $x$ and $y$
-
'’parallel’’ $x \ \ y$ - $x \ \ y \iff x > y \land y > x$ - i.e. can see both $…xy…$ and $…yx…$ - cannot put a place for such $x$ and $y$ - if we placed, we’d impose some order on them
-
this is symmetric relation ($a \ \ b \to b \ \ a$) - ‘‘unrelated’’ $x \ # \ y$ - $x \ # \ y \iff x \not > y \land y \not > x$
- i.e. there are no traces $…xy…$ nor $…yx…$
- this is also symmetric relation $x \ # \ y \to y \ # \ x$
The set of all relations for a log $L$
- is called the ‘‘footprint’’ of $L$
Example
For example,

- the log is $L_1 = [abcd, acbd, ef]$
- $a > b, a > c, b > c, b > d, c > b, c > d, e > f$
- $a \to b, a \to c, b \to d, c \to d, e \to f$
-
$b \ \ c$
Consider another example:
- $L_2 = [abcd, acbd, aed]$
- The footprint can be represented with a table
- in rows we have the left-hand-side operand, in columns - the right-hand-side operand
| $a$ | $b$ | $c$ | $d$ | $e$ | $a$ | $#$ | $\to$ | $\to$ | $#$ | $\to$ | $b$ | $\leftarrow$ | $#$ | $ | $ | $\to$ | $#$ | $c$ | $\leftarrow$ | $ | $ | $#$ | $\to$ | $#$ | $d$ | $#$ | $\leftarrow$ | $\leftarrow$ | $#$ | $\leftarrow$ | $e$ | $\leftarrow$ | $#$ | $#$ | $\to$ | $#$ |
$\alpha$ Algorithm
With these relations we define the $\alpha$ algorithm as follows.
$\alpha(L):$
- extract all transition names from $L$ to set $T$
- let $T_I$ be the set of all initial transitions and $T_O$ the set of all end transitions
- find all pairs of sets $(A, B)$ such that
- $t_A \in A$ should be connected to all $t_B \in B$ via some place $p$
- $\forall a \in A$ and $\forall b \in B$ holds that $a \to b$
- $\forall a_1, a_2 \in A: a_1 \ # \ a_2$ and $\forall b_1, b_2 \in B: b_1 \ # \ b_2$
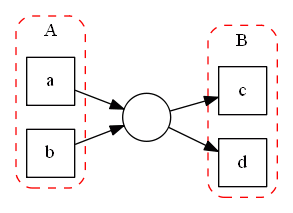
- in this example: $a \ # \ b, c \ # \ d, a \to c, a \to d, b \to c, b \to d$
- in other words: all transitions from $A$ put tokens to the place $p$, and transitions of $B$ take tokes from $p$
- once found all such sets, we retain only the maximal ones
- a ‘‘maximal set’’ contains the maximal possible number of elements that can be connected via single place
- for each such pair $(A, B)$ we connect all elements from $A$ with all elements from $B$ with one single place $p_{(A, B)}$
- then we also connect appropriate transitions with the input and output places
- finally we connect the start place $i$ to all transitions from $T_I$
- and all transitions from $T_O$ with the final state $o$
Example
for the log $L_2 = [abcd, acbd, aed]$ the footprint is
| $a$ | $b$ | $c$ | $d$ | $e$ | $a$ | $#$ | $\to$ | $\to$ | $#$ | $\to$ | $b$ | $\leftarrow$ | $#$ | $ | $ | $\to$ | $#$ | $c$ | $\leftarrow$ | $ | $ | $#$ | $\to$ | $#$ | $d$ | $#$ | $\leftarrow$ | $\leftarrow$ | $#$ | $\leftarrow$ | $e$ | $\leftarrow$ | $#$ | $#$ | $\to$ | $#$ |
- $T_I$: the set of all first transitions in the log,
- in the table, for such transitions we don’t have any incoming edges
- i.e. it has only $\leftarrow$, no $\to$ in its column
- $T_I = {a}$
- $T_O$: the set of all last transitions in the log
- no outcoming edges, only incoming - in the rows
- $T_O = {d}$
With this table, using $\to$ and $| |$ relations we can draw the following graph: |- 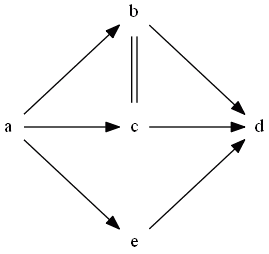
- (a directed edge represents $\to$ relation, undirected double edge represents $| |$) | Now with this graph can enumerate the maximal sets $A$ and $B$
- recall that for sets $A$ and $B$
- $\forall a_1, a_2 \in A: a_1 \ # \ a_2$
- $\forall b_1, b_2 \in B: b_1 \ # \ b_2$
- $\forall a_1 \in A, \forall b_1 \in B: a_1 \to b_1$
| | $A$ | $B$ | (1) | ${a}$ | ${b, e}$ || (2) | ${a}$ | ${c, e}$ || (3) | ${b,e}$ | ${d}$ || (4) | ${c,e}$ | ${d}$ | Note that $b$ and $c$ cannot belong to the same set
- they are parallel
Based on these sets
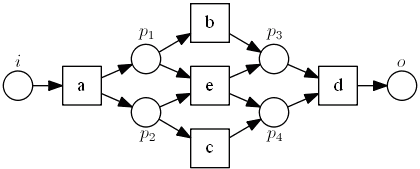
- we add 4 places for each pair $(A, B)$ to connect all elements from $A$ with all elements from $B$ with one place
- and we add 2 more places: the start place $i$ and the final state $o$
| | $A$ | $B$ | | $p_1$ | ${a}$ | ${b, e}$ | 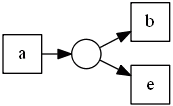 || $p_2$ | ${a}$ | ${c, e}$ |
|| $p_2$ | ${a}$ | ${c, e}$ | 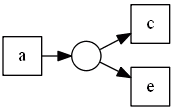 || $p_3$ | ${b,e}$ | ${d}$ |
|| $p_3$ | ${b,e}$ | ${d}$ | 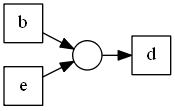 || $p_4$ | ${c,e}$ | ${d}$ |
|| $p_4$ | ${c,e}$ | ${d}$ | 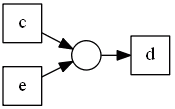 |
So we have:
|
So we have:
Limitations
There are some limitations of the $\alpha$ algorithm.
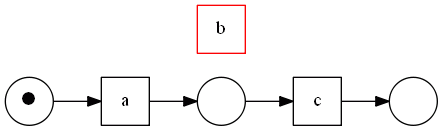
=== Loops of Length One === If there are short loops of length one, $\alpha$ cannot re-discover them.
suppose we have the following log
- $[ac, abc, abbc, abbbc]$
- model that generated this log:
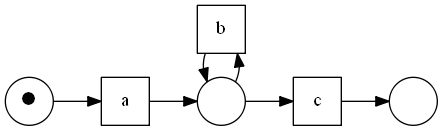
but here is what $\alpha$ finds:
reason
- the step for finding sets $A$ and $B$
- in this case we want that $b \in A$ and $b \in B$
- but it cannot happen because $b \ \not # \ b$
Loops of Length Two
If there are short loops of length two, $\alpha$ cannot re-discover them either.
suppose we have the following log
- $[abd, abcbd, abcbcbd]$
- model that generated this log:
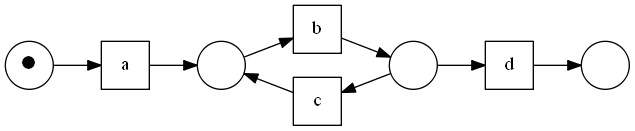
but here is what $\alpha$ finds:
reason
-
here we think that $b \ \ c$, since $b > c$ and $c > b$ - but it’s not the case
Other Loops
No problems
Non-Local Dependencies
Non-Local dependencies results from some process constraints.
- These constraints cannot be captured by the $\alpha$ algorithm
-
They are not visible in the logs - (It’s actually the problem of many Process Mining algorithms, not just $\alpha$)
For example,
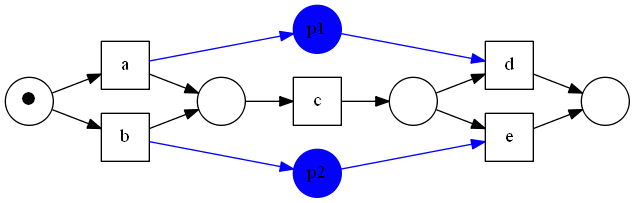
- log: $[acd, bce]$
- If I came to work by car ($p_1$) - I will leave by car
- If I came to work by train ($p_2$) - I will leave by train
- the blue places represent non-local dependencies that will not be discovered
In general, the constraints the difficult constraints are:
We want to avoid such constructs in out workflow nets because they cannot be discovered.
A workflow net belongs to ‘‘Structured Workflow Net’’ (SWF) class of workflow nets if
- it doesn’t have such constructions
- it has no implicit places
$\alpha$ mines all SWF nets except for ones with short loops
The Alpha Plus Algorithm
$\alpha^+$ handles short loops
Loops of Length 2
First, let’s have a look at loops of length 2.
Recall our example:

- $[abd, abcbd, abcbcbd]$
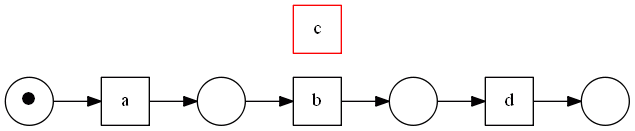
We see that the problem with these loops is incorrect assumption that $b | | c$. |- because from the logs we see that $b > c$ and $c > b$, therefore we cannot cay $b \to c$ based on the defined relations
- need to define new relations that can capture such behavior
We need another notion of log completeness to handle such loops:
for a workflow net $N$ a log is loop-complete if
- it is complete
- there’s enough information to detect loops of length two (i.e. we see sequences of $…t_1 t_2 t_1…$ s.t. $t_1 \ne t_2$)
Example
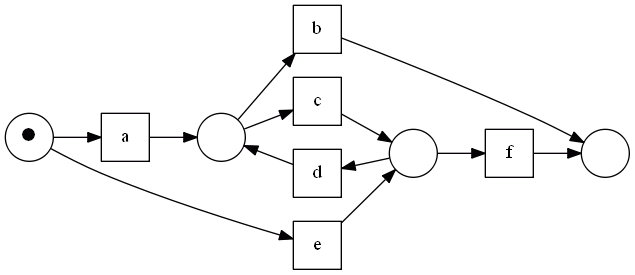
- a loop-compete log in this case contain one or more traces with $…cdc…$ and $…dcd…$
New Ordering Relations
Recall that we need to be able to distinguish $a \to b$ and $a \ | | \ b$, which is not possible for loops of length 2 with the old notion of these relations. |
Same as previously
- $a > b \iff$ we see trace $…ab…$
- $a \ # \ b \iff a \not > b \land b \not > a$
New relations
- $a \ \triangle \ b \iff$ there is a subsequence $…aba…$ in the logs
- $a \ \diamondsuit \ b \iff$ there are sequences $…aba…$ and $…bab…$
And we redefine the relations that cause the error
- $a \to b \iff a > b \land (b \not > a \lor a \ \diamondsuit \ b)$
- this way we can correctly identify the ‘‘follow’’ relation when there’s a loop of length 2
-
$a \ \ b \iff a > b \land b > a \land a \ \not \diamondsuit \ b$ - by adding the last condition way we don’t misidentify the ‘‘parallel’’ relation
However, there’s one caveat. Short loops of length one also can produce such sequences
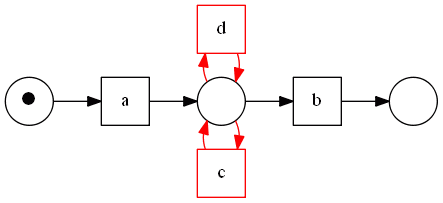
- therefore at this step we assume that the net is ‘‘one-loop-free’’ - i.e. it does not contain loops of length 1
- if it’s not the case, we can turn our worflow net into ‘‘one-loop-free’’ by removing all transitions that create these loops. we discuss below why it is possible.
- we will address this problem during pre-procession step
- also note that for one-loop-free workflow nets $a \ \triangle \ b \Rightarrow b \ \triangle \ a$
Loops of Length 1
a transition is ‘‘one-loop’’ transition if it participates in a loop of length 1
Properties
- one-loop transition cannot be connected to the input or output places (otherwise such a network would not be a workflow net)
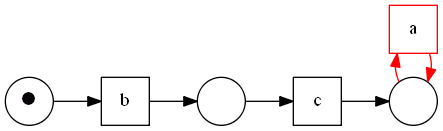
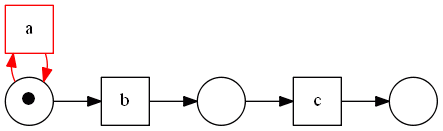
We can safely remove such a transition from a workflow net
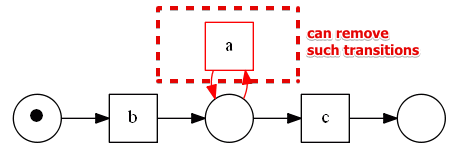
- it will clearly not affect other transitions and the net will remain sound
- we can proof this statement by checking the reachability graph of the net with these transitions and without them - in both cases the states of a graph will be the same
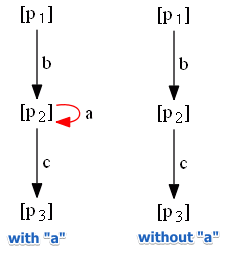
For example:
- consider the net above
- if we remove transition $a$, we will get the following Reachability Graph
Idea:
- handle these transitions during pre- and post-processing stages
- identify ‘‘one-loop’’ transition $t$ by searching for patterns like $…tt…$
determine the places $p$ to which it should be connected to do it we check:
what are the transitions $a$ s.t.
- $t > a \land a \not > t$
- i.e. transitions $a$ that are followed by $t$, but don’t follow $t$ themselves
- $p$ should be an input place for $a$ and output place for $t$
- $b > t \land t \not > b$
- transitions $b$ that follow $t$, but are not followed by $t$
- $p$ should be an output place for $b$ and input place for $t$
$\alpha^+$ Algorithm
$\alpha^+(W)$:
- let $T$ be all transitions found in the log $W$
- identify all one-loop transitions and put them into set $L1L$
- let $T’$ be all non-one-loop transitions: $T’ \leftarrow T - L1L$
- let $F_{L1L}$ be the set of all arcs to transitions from $L1L$
- : it consists of:
- all transitions $a$ that happen before $t$: $a \in T’$ s.t. $a > t$
- all transitions $b$ that happen after $t$: $b \in T’$ s.t. $t > b$
- now remove all occurrences of transitions $t \in L1L$ from the log $W$, let the result be $W^{-L1L}$
- run the $\alpha$ algorithm on $W^{-L1L}$: $\alpha(W^{-L1L})$
- reconnect one-loop transitions back: add all transitions and from $L1L$ and arcs from $F_{L1L}$ to transitions and arcs discovered by $\alpha$
Examples of Petri Nets
Examples of petri-nets that $\alpha^+$ can re-discover (and $\alpha$ cannot):
Conclusions
There have been made some assumptions:
- perfect information (the log completeness)
- absence of noise in the logs
usually it’s not the case in real life and different mining algorithms should be used
- such as Genetic Miner
Examples
- The Housing Agency Workflow was successfully re-discovered with the $\alpha^+$ algorithm
Links
Sources
- Medeiros, van Dongen, van der Aalst and Weijters. Process Mining: Extending the alpha-algorithm to Mine Short Loops, 2004 [http://www.processmining.org/blogs/pub2004/process_mining_extending_the_alpha-algorithm_to_mine_short_loops]
- van der Aalst. Process Mining: Discovery, Conformance and Enhancement of Business Processes, 2011 [http://www.processmining.org/book/start]
- Business Process Management (ULB)