Process Mining
Suppose we have a log of our process, but do not have the model of this process
- the ‘‘process mining’’ is a way to find a process from the logs
- the model can be a Workflow Net, YAWL or BPMN model.
Definitions
A process mining algorithm is a function that
- maps an event log $L$ to some workflow model
- ideally the model should be sound
play-in = process discovery
- event logs $\to$ workflow model
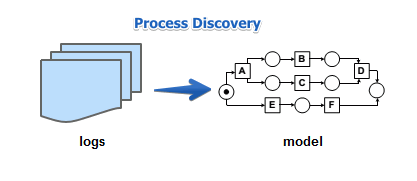
the ‘‘ability to rediscover’’
- is a property of a process mining algorithm to discover a model of some process
- from logs that have been generated from this model
- i.e. in case of Petri Nets, if $N$ is the original model and $N’$ is the discovered model, then $N \equiv N’$
Some Notes
Usually, first a Petri Net model is discovered
Measures
There are four conflicting criteria
- Fitness
- the discovered network should allow the behavior seen in the logs
- Precision
- the discovered network should not allow the behavior not seen in the logs
- too precise $\to$ bad generalization
- Generalization
- the discovered model should generalize the behavior seen in the logs
- Simplicity
- it should be as simple as possible
- too simple $\to$ low fitness

- The main challenge of Process Mining is that all these criteria are conflicting:
- It’s really hard to simultaneously satisfy all of them
- this makes Process Mining to be a Multi-Objective Optimization problem
Fitness
Can we replay the log?
- we try to replay each sequences from the logs
- so for each we see if this sequences is allowed
- if each sequence can be replayed - 100% fitness
- special notion for fitness is also defined for the Genetic Process Miner
Precision
Do we underfit the log?
- play out the model, capture logs
- see what’s generated and compare to the original logs
- is it far? (need to have some distance measure)
if produced logs $\subseteq$ original logs
- then we have 100% precision
Generalization
Do we overfit the log?
- very hard to measure
Simplicity
The simpler the model - the better
- may add some penalty for each added place
- (the more places we add, the more complex the model becomes)
Examples
The Flower Model

- this model in at the one end of spectrum
- very simple
- good fitness: every possible trace can be reproduced
- generalization: allows a lot of behavior
- but precision is very low: it allows a lot of behavior not seen in the logs
The Enumerating Model

- another end of the spectrum
- behavior only seen in the logs: not more, not less
- good fitness and good precision
- no generalization at all
- no simplicity
Conclusions
So Process Mining is difficult
- it’s a Multi-Objective Optimization problem
- there are no negative examples
- the search space is too complex
- logs typically show only a fraction of possible behavior
Algorithms
These algorithms let you find a Petri Net from logs
- $\alpha$ and $\alpha^+$ algorithms - simple, but tend to overfit, very susceptible to noise in logs
- Region-Based Process Miner - state-based approach, still susceptible to noise
- Genetic Process Miner - good performance, much less susceptible to noise