Overfitting

Overfitting

'’Overfitting’’ (or ‘‘high variance’’) - if we have too many features, the learning hypothesis may

• fit the training set very well (with cost function $J(\theta) \approx 0$),
• but fail to generalize to new examples (predict for new data)

Generalization Error

Cross-Validation

Best way to see if you overfit:

• split data in training and test set
• train the model on training set
• evaluate the model on the training set
• evaluate the model on the test set
• generalization error: difference between them, measures the ability to generalize

It’s clear that a model overfits when we plot the generalization error

• 
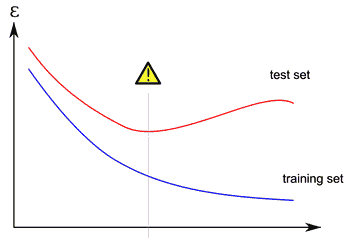
• we have low error on the training data, but high on the testing data
• may perform Machine Learning Diagnosis to see that

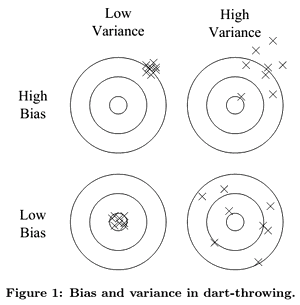
High Variance vs High Bias

Generalization error can be decomposed into bias and variance

• bias: tendency to constantly learn the same wrong thing
• variance: tendency to learn random things irrespective to the input data

Dart throwing illustration:

Underfitting

• high bias, low variance
• you’re always missing in the same way

example:

• predict always the same
• very insensible to the data

• the variance is very low

  (0)

  - but it has high bias - it’s wrong

Examples

Multivariate Linear Regression

Suppose we have a set of data

• 
• We can fit the following Multivariate Linear Regression model
• linear: $\theta_0 + \theta_1 x$, likely to underfit (high bias)
• quadratic: $\theta_0 + \theta_1 x + \theta_2 x^2 $

• extreme: $\theta_0 + \theta_1 x + \theta_2 x^2 + \theta_3 x^3 + \theta_4 x^4 $

  

Logistic Regression

Same applies for Logistic Regression

• Suppose we have the following set
• 
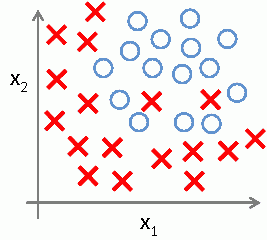
• We may underfit with just a line
  • $g(\theta_0 + \theta_1 x_1 + \theta_2 x_2)$
• We may perform just right, but missing some positive examples
  • $g(\theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_1^2 + \theta_4 x_2^2 + \theta_5 x_1 x_2)$
• Or we may overfit using high-polynomial model
  • $g(\theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_1^2 + \theta_4 x_2^2 + \theta_5 x_1 x_2 + \theta_6 x_1^2 x_2 + \theta_7 x_1 x_2^2 + \theta_8 x_1^2 x_2^2 + \theta_9 x_1^3 + …)$
• 

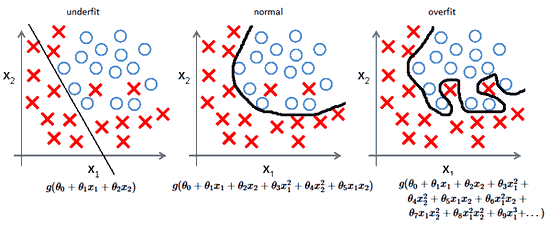
The problem with it

• overly high polynomial

• it can fit anything

  - it overfits - results in high variance

Diagnosing

How to Diagnose the Problem

To identify overfitting we can use Machine Learning Diagnosis:

• Cross-Validation
• and Learning Curves

How to Address the Problem

• plotting - doesn’t work with many features
• reducing the number of features
  • manually select features to keep
  • Model Selection algorithm (chooses good features by itself)
  • but it may turn out that some of the features we want to throw away are significant
  • Principal Component Analysis
• Regularization
  • keep all the features but reduce the magnitude of parameters
• Cross-Validation
  • test your hypotheses on cross-validation set

Sources

• Machine Learning (coursera)
• Data Mining (UFRT)
• Introduction to Data Science (coursera)
• Domingos, Pedro. “A few useful things to know about machine learning.” [http://homes.cs.washington.edu/~pedrod/papers/cacm12.pdf]