Decision Tree Exercises
These are exercises given at Decision Engineering (ULB)
Exercise 1: Football Team Campaign
An university thinks whether to hold a company to promote their football team
- The team has had winning seasons 60% of the time in the past
- if the team will have a winning season ($W$) then the university raise 3 mln usd
- if the team will have a losing season ($L$) then they lose 2 mln usd
- if no campaign is taken - there will be no losses
- they have to decide whether to take the campaign or not
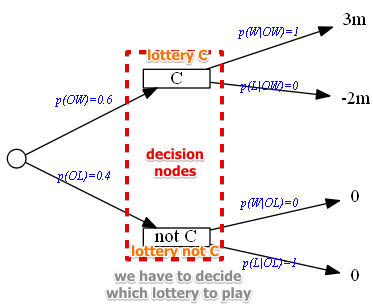
Take or Not?
We can create a simple lottery that describes the process:
- $W$ - win, $p(W) = 0.6$
- $L$ - lose, $p(L) = 1 - 0.6 = 0.4$

Now we need to compare this lottery with another one:
- no campaign, no losses

How we compare these two lotteries?
- with Expected Values for Lotteries
- launch: $E(C) = 3 \cdot 0.6 + (-2) \cdot 0.4 = 1$
- not launch: $E(\overline{C}) = 0$
- based on expected value we decide to launch
Perfect Information
Suppose we hired an Oracle - someone who knows for sure what is going to happen
- how much we want to pay for such an Oracle?
Oracle
- based on past statistics we assume that the oracle will say that
- team loses ($OL$) 40% of time
- them wins ($OW$) 60% of time
- Oracle is always right:
- if he tells that the team will win ($OW$) it wins, and never loses
- $p(W \mid OW) = 1, p(L \mid OW) = 0$
- the same with losing:
- $p(W \mid OL) = 0, p(L \mid OL) = 1$
So we get this perfect information tree
Now we can calculate the expected gain from having the perfect information:
- $E(PI) = 0.6 \cdot 1 \cdot 3 + 0.6 \cdot 1 \cdot (-2) + 0.4 \cdot 0 \cdot 0 + 0.4 \cdot 1 \cdot 0$
- $E(PI) = 1.8$
- so we may pay him as much as 1.8 - as long as we are not losing, it’s good
An Expert Consultation
But suppose we hire a human being who makes mistakes to help us to predict the outcome
- the consultancy of a football guru costs 0.1
- we have some statistics about the guru:
- in the past his predictions for winning seasons was correct 75% of time
- for losing seasons - 80% of time
Model:
- we know the statistics about him:
- $p(GW \mid W) = 0.75$ - the probability of the guru saying that the team wins when it indeed wins
- $p(GL \mid L) = 0.8$ - the probability of the guru saying that the team loses when it indeed loses
- we don’t know the probabilities
- but we can calculate them
Here’s our decision tree:
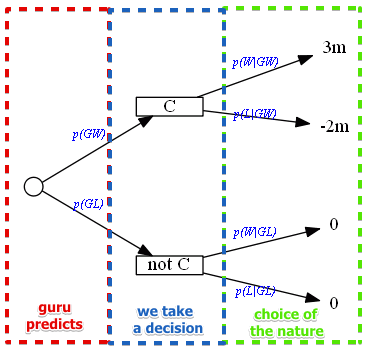
- need to calculate the probabilities
Calculating the probabilities
- $p(GW)$
- $p(GW \land \underbrace{[W \lor L]}_\text{true}) = p([GW \land W] \lor [GW \land L]) = …$
- the events $[GW \land W]$ and $[GW \land L]$ are independent, so can do the following
- $… = p(GW \land W) + p(GW \land L) = …$
- $… = p(GW \mid W) \cdot p(W) + p(GW \mid L) \cdot p(L) = …$
- now we know all the values - so put them there
- $… = 0.75 \cdot 0.6 + 0.2 \cdot 0.4 = {\color{blue}{0.53}} $
- $p(GL)$
- $p(GL) = 1 - p(GW) = 0.47$
- $p(W \mid GW)$ and $p(L \mid GW)$
- $p(W \mid GW) = \cfrac{p(W \land GW)}{p(GW)} = \cfrac{p(GW \mid W) p(W)}{p(GW)} = …$
- $… = \cfrac{0.75 \cdot 0.6}{0.53} = 0.8491$
- $p(L \mid GW) = 1 - p(W \mid GW) = 1 - 0.8491 = 0.1509$
- no need to compute $p(W \mid GL)$ and $p(L \mid GL)$
- since in this case we don’t take any action
- and the outcome in both cases is 0
Now we can compute the expected value:
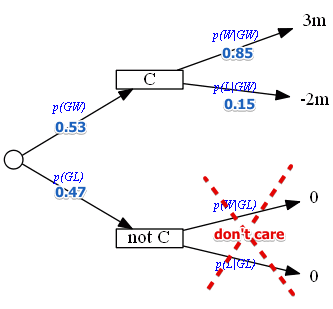
- $E(C) = 3 \cdot 0.8491 - 2 \cdot 0.1509 = 2.2455$
- $E(G) = 0.53 \cdot 2.2455 = 1.1901$
- so this is the expected outcome if we pay the guru
- it costs 0.1 so it’s reasonable to pay him
- the net value is then $1.1901 - 0.1 = 1.0901$
Exercise 2: Sell Now or Later
A raider acquired a textile company along with its plant. There are 3 alternatives:
- $E$: expand the plant and produce the materials for military (with little foreign competition $G$)
- $Q$: maintain the status quo - continue as it is (heavy foreign competition $P$)
- $S$: sell the plant now
So the model is:
- alternatives are $E, Q, S$
- the states of nature is $G, P$ - good and poor competitive conditions
The evaluation table (in $10^5$ USD):
| Decision | Good Conditions | Poor Conditions | $E$ | 8 | 5 | $M$ | 13 | -1.5 | $S$ | 3.2 | 3.2 |
Decision Under Uncertainty
If we are totally uncertain about the outcomes, we may apply the methods from Decision Under Uncertainty
Maximin and Maximax
| $c$ | $G$ | $P$ | max | min | $E$ | 8 | 5 | 8 | 5 || $M$ | 13 | -1.5 | 13 | -1.5 || $S$ | 3.2 | 3.2 | 3.2 | 3.2 || | | | 13 | 5 | For maximin we take $E$, for maximax we take $M$
Minimax Regret
We build the following regret table:
| $R$ | $G$ | $P$ | max | $E$ | 5 | 0 | 5 || $M$ | 0 | 6.5 | 6.5 || $S$ | 9.8 | 1.8 | 9.8 | The option that minimizes the regret is $E$
Hurwitz’s Index
Suppose $\alpha = 0.7$ ($1 - \alpha = 0.3$)
- $\alpha$ in this case refers to the pessimistic (min) condition
- usually we put more weight on the min
| $c$ | $G$ | $P$ | max | min | index | $E$ | 8 | 5 | 8 | 5 | 0.3 * 8 + 0.7 * 5 = 5.9 | $M$ | 13 | -1.5 | 13 | -1.5 | 0.3 * 13 + 0.7 * (-1.5) = 2.89 | $S$ | 3.2 | 3.2 | 3.2 | 3.2 | 0.3 * 3.2 + 0.7 * 3.2 = 3.2 |
In this case $E$ is the best option
Laplace Rule
We assign equal probabilities to the outcomes
- $p(G) = p(P) = 0.5$
| $c$ | $G$ | $P$ | index | $E$ | 8 | 5 | 0.5 * 8 + 0.5 * 5 = 6.5 | $M$ | 13 | -1.5 | 0.5 * 13 + 0.5 * (-1.5) = 5.75 | $S$ | 3.2 | 3.2 | 0.5 * 3.2 + 0.5 * 3.2 = 3.2 |
Again $E$ is the best option
Decision Under Risk
Assume now that we can estimate the probability of each state of nature
- $p(G) = 0.7$ and $p(P) = 0.3$
Expected Value
- $E(E) = 0.7 \cdot 8 + 0.3 \cdot 5 = 7.1$
- $E(M) = 0.7 \cdot 13 + 0.3 \cdot (-1.5) = {\color{blue}{8.65}}$
- $E(S) = 0.7 \cdot 3.2 + 0.3 \cdot 3.2 = 3.2$
We want to maximize it, so
- we take $M$
Expected Opportunity Lost
This is the same, but we calculate Expected Value on the Regret Table:
- in this case we want to minimize the regret
Expected Values
- $E(E) = 0.7 \cdot 5 + 0.3 \cdot 0 = 3.5$
- $E(M) = 0.7 \cdot 0 + 0.3 \cdot 6.5 = {\color{blue}{1.95}}$
- $E(S) = 0.7 \cdot 9.8 + 0.3 \cdot 1.8 = 7.4$
We want to minimize it, so
- we take $M$
Perfect Information
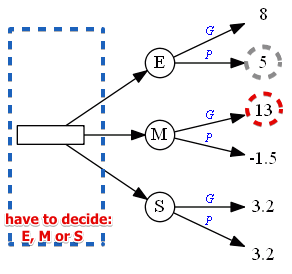
Suppose we have the perfect information
- so if we know that $G$ happens, we choose $M$
- if $P$ happens - we choose $E$
Then the expected value of the perfect information is
- $EV(PF) = 0.7 \cdot 13 + 0.3 \cdot 5 = 1.06$
Decision Tree (Decision Theory)
Now suppose that we hire a consultant
- he will report whether to wait for $G$ or $P$
- $RP$ report says to wait for $P$, $RG$ - report says to wait for $G$
We know that the consultant has not always been right:
- $p(RG \mid G) = 0.7$ - in 70% he reported good conditions when conditions indeed were good
- $p(RP \mid P) = 0.8$ - in 80% he reported bad conditions when conditions were indeed bad
- can infer that $p(RP \mid G) = 0.3$ and $p(RG \mid P) = 0.2$
- recall that $p(G) = 0.7$ and $p(P) = 0.3$
So we need to determine the posterior probabilities
- (by using Conditional Probability rules)
- $p(RG) = p(G) \cdot p(RG \mid G) + p(P) \cdot p(RG \mid P) = 0.7 \cdot 0.7 + 0.3 \cdot 0.2 = 0.55$
- $p(RP) = 1 - p(RG) = 0.45$
- $p(G \mid PG) = \cfrac{ p(G) \cdot p(RG \mid G) }{ p(RG) } = \cfrac{0.7 \cdot 0.7}{0.55} = 0.89$
- $p(P \mid PG) = 1 - 0.89 = 0.11$
- $p(P \mid RP) = \cfrac{ p(P) \cdot p(RP \mid P) }{ p(RP) } = \cfrac{ 0.3 \cdot 0.8}{0.45} = 0.53$
- $p(G \mid RP) = 1 - p(P| RP) = 0.47$ | We create a decision tree based on that
- note that if report is good, then the best is to take $M$ (it dominates all the other alternatives)
- the same for bad: $E$ dominates all the other
- therefore we need to include only there alternatives
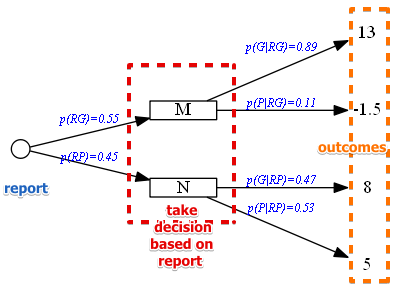
Now we can calculate the expected value when hiring a consultant
- $E(M) = 0.89 \cdot 13 - 0.11 \cdot 1.5 = 11.405$
- $E(N) = 0.47 \cdot 8 + 0.53 \cdot 5 = 6.41$
- $E(\text{total}) = 0.55 \cdot 11.405 + 0.45 \cdot 6.41 = 9.157$
- this value is what you’ll earn on average when hiring a consultant