ML Wiki

Multi-Objective Optimization

In contrast to Uni-Objective Optimization problems, in Multi-Objective Optimization problems there are multiple

An usual model is:

• $\text{opt} f_1(x), ..., f_q(x), x \in A$
• but usually in this case there is no single optimal solution - but a set of solutions where you cannot say which one is better

Example:

• suppose you want to buy a flat
• there are 2 criteria: cost and comfort
• you want to minimize the cost and maximize the comfort
• 
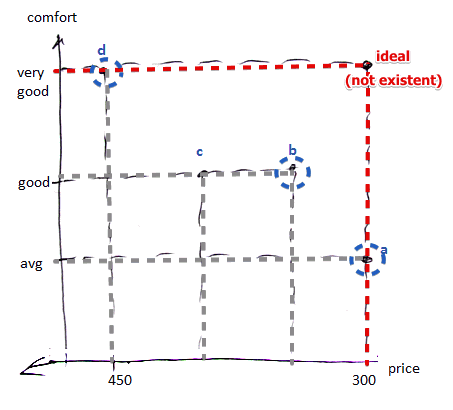
• note that you cannot say that $d$ is better than $b$ or better than $a$
• but $c$ is clearly dominated by $b$: it's as comfortable as $c$, but cheaper
• the set of the best alternatives is called the Pareto-optimal set of alternatives

Multi-Criteria Problem

We have $q$ criteria and $n$ items

	Criterion 1	Criterion 2	...	Criterion $q$
Item 1	100	Medium	...	8
Item 2	100	Medium	...	8
...	...	...	...	...
Item $n$	55	Very Bad		8

Goal: to rank the items

• there are lots of conflicting criteria (like price and comfort)
• there are different units and scales
• the single optimal solution does not exist

Instead of "Item" it can be "Action", "Alternative", etc

Formally we can write it as:

• objective: $\text{opt} z(x)$
• $z: \mathbb{R}^n \to \mathbb{R}^m$
• constraints: $g_i(x) \geqslant 0, x \in \mathbb{R}^n$

Link to Voting Theory

But it is possible to draw a direct parallel with Voting Theory!

	Voter 1	Voter 2	...	Voter $q$
Candidate 1	100	Medium	...	8
Candidate 2	100	Medium	...	8
...	...	...	...	...
Candidate $n$	55	Very Bad		8

So these two problems are similar:

• Each voter ranks all candidates (alternatives)
• We apply some voting mechanism and find the global preference (the "best" alternative)
• All properties of Voting Theory are still available:
  • Unanimity,
  • Monotonicity,
  • Independence to Third Alternatives
  • and others

However there are differences:

• Not all criteria have the same weight
  • in Voting Theory all votes are equally important
  • here some criteria may be more important than others
• We need more information than just ranking
  • There are different scales
  • Since the scales can be numerical, we can compare the intensity of preference

Multi-Objective Optimization Problems

• Multi-Objective Knapsack Problem
• Flowshop Problem
• Portfolio Management
• Waste Utilization Problem

Choosing the Solution

Suppose we have obtained the Pareto-optimal set of solutions. How do we choose the "best" solution?

There are several approaches:

• Weighted Sum Model
• Ideal Point Model

Multi-Criteria Decision Aid

Also MCDA is used for that:

• find the Pareto-optimal solutions
• apply MCDA to find the best one

Sources

• Decision Engineering (ULB)