Vector Spaces

Vector Spaces

Suppose we have a set $V$ and elements $\mathbf v_1, …, \mathbf v_i … \in V$

• we define ‘‘addition’’ on $V$ where we map any pair $\mathbf v_i, \mathbf v_j \in V$ to a value $\mathbf v_i + \mathbf v_j$
• and we define the operation ‘‘scalar multiplication’’ where for any scalar number $c$ and a vector $\mathbf v \in V$ we have a value $c \cdot \mathbf v$

So, what can we do with elements in a vector space?

• add two elements
• multiply them by a scalar
• it means we should be able to take linear combinations of elements in the space

Axioms

The elements of $V$ are ‘‘vectors’’ and $V$ is a space if the axioms hold

• commutativity: $\mathbf v_i + \mathbf v_j = \mathbf v_j + \mathbf v_i$
• associativity: $(\mathbf v_i + \mathbf v_j) + \mathbf v_k = \mathbf v_j + (\mathbf v_i + \mathbf v_k)$
• there exists an element $\mathbf 0 \in V$ s.t. $\mathbf 0 + \mathbf v = \mathbf v$
• for any element $\mathbf v$ there exists the ‘‘opposite’’ $-\mathbf v$ s.t. $\mathbf v + (-\mathbf v) = \mathbf 0$
  • therefore can define ‘‘difference’’ as $\mathbf v_1 - \mathbf v_2 = \mathbf v_1 + (-\mathbf v_2)$

multiplication on scalars ($c$’s are scalars):

• $c (\mathbf v_1 + \mathbf v_2) = c \mathbf v_1 + c \mathbf v_2$
• $(c_1 + c_2) \mathbf v = c_1 \mathbf v + c_2 \mathbf v$
• $(c_1 \cdot c_2) \cdot \mathbf v = c_1 \cdot (c_2 \cdot \mathbf v)$
• $1 \cdot \mathbf v = \mathbf v$

Implications:

• $c \cdot \mathbf 0 = \mathbf 0$
• $0 \cdot \mathbf v = \mathbf 0$
• if $c \cdot \mathbf v = \mathbf 0$ then either $c = 0$ or $\mathbf v = \mathbf 0$
• $c \cdot (- \mathbf v) = - c \cdot \mathbf v$
• $(- c) \cdot \mathbf v = - c \cdot \mathbf v$
• $c (\mathbf v_1 - \mathbf v_2) = c \mathbf v_1 - c \mathbf v_2$
• $(c_1 - c_2) \mathbf v = c_1 \mathbf v - c_2 \mathbf v$

Example: Coordinate Spaces

• $\mathbb R^2$ - real numbers (“$x/y$ plane”)
• e.g. $\begin{bmatrix} 3
  2 \end{bmatrix}$, $\begin{bmatrix} 0
  0 \end{bmatrix}$, $\begin{bmatrix} \pi
  e \end{bmatrix}$, …
• there’s a picture that goes with $\mathbb R^2$
• 
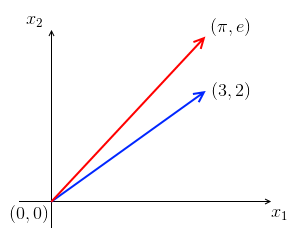
• so, we can picture every vector in the space
• (same for $\mathbb R^3$)

Vector Subspaces

A subspace of a vector space should form a space on it’s own.

Any line through the origin:

• 
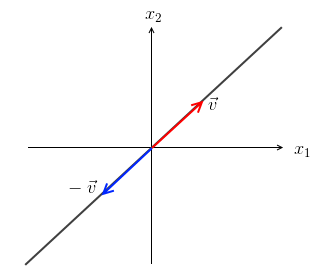
• is it a vector space?
• yes. We can take any scalar, and the result will still be on the line
• if the line is not through the origin, then multiplying by 0 will bring us out of the space - so the origin must be included

For a Matrix there are Four Fundamental Subspaces:

• Column Space
• Row Space
• Nullspace
• Left Nullspace

Vector Spaces

Matrix Vector Spaces

A matrix space is also a vector space, where elements are matrices of the same dimensionality: we can multiply matrices by a scalar and can add two matrices of the same dimension.

• Inner Product: e.g. $\langle A, B \rangle = \sum_{ij} a_{ij} b_{ij}$

• norm: e.g. Frobenius Norm: $| A |_F = \langle A, A \rangle$

Function Spaces

In a function space, the “vectors” are functions:

• we can define an Inner Product as $\langle f, g \rangle = \int\limits_{-\infty}^{\infty} f(x) \, g(x) \, dx$ with Integral instead of sum
• and we define orthogonality as $\langle f, g \rangle = 0$

Sources

• Linear Algebra MIT 18.06 (OCW)
• Курош А.Г. Курс Высшей Алгебры