$kd$-Trees
- it’s a generalization of binary search trees to multidimensional data
- Main Memory structure (not Secondary Storage| ) | |
Classical $kd$-Tree
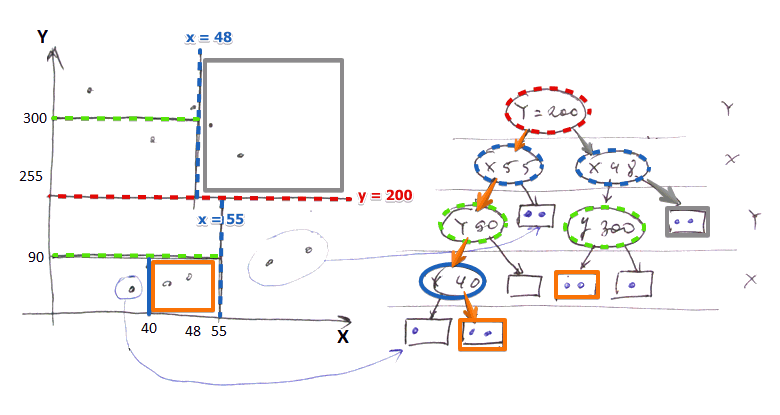
- '’split attributes’’ at different levels are different
- in the example: first split by $Y$, then by $X$, then by $Y$…
- interior nodes of the tree contain
- attribute on which we divided the space
- a dividing value
-
left and right pointers (only 2 ) - leaves are blocks with records
Operations
Lookup
- similar to binary search trees
- but need to use only attribute specified in a interior node of the tree
Insertion
- look up the block
- if there’s room - put it there
- not - split into 2
- we divide by the most appropriate attribute
- and create a new interior node that points to the split halves
Queries
Good for See Multi-Dimensional Indexes#Typical Queries
- Point Queries (just lookup)
- Partial Match
- suppose we specified only $Y$
- then if it’s not $Y$ follow both left and right pointers
- if it’s $Y$ then use the dividing value in the node to decide whether to go left or right
Reasonable Support
- Nearest-Neighbor
Adaptation to Secondary Storage
The described algorithm is for Main Memory, not for disk
2 ways to adapt
- Multi-Way Branches
- like in B-Tree: $n$ keys, $n + 1$ pointers
- hard to merge to keep it balanced
- Several Nodes Per Block
- Keep 2 children per block as described
- but store several nodes per one block
- to minimize I/O it’s better to put in the same block records that are likely to be accessed together
- For example, a node and it’s descendants
See also
Sources
- Database Systems Architecture (ULB)
- Database Systems: The Complete Book (2nd edition) by H. Garcia-Molina, J. D. Ullman, and J. Widom