SNN Clustering
The goal:
- find clusters of different shapes, sizes and densities in high-dimensional data
- DBSCAN is good for finding clusters of different shapes and sizes, but it fails to find clusters with different densities
- it will find only one cluster:
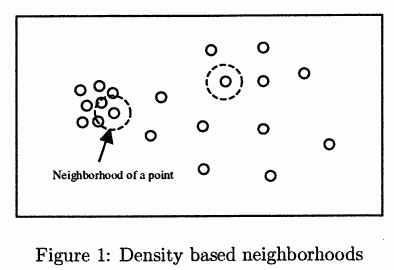
- (figure source: Ertöz2003)
Distance:
- Euclidean Distance is not good for high-dimensional data
- use different similarity measure in terms of KNNs - “Shared Nearest Neighbors”
- then define density in terms of this similarity
Jarvis-Patrick Algorithm
“Jarvis-Patrick” algorithm, as in Jarvis1973
Step 1: SNN sparsification:
- construct an SSN Graph from data matrix as follows
- if $p$ and $q$ have each others in the KNN list
- then create a link between them
Step 2: Weighting
-
weight the links with $\text{sim}(p, q) = \big \, \text{NN}(p) \ \cup \ \text{NN}(q) \, \big $ - where $\text{NN(p)}$ and $\text{NN(q)}$ are $k$ neighbors of $p$ and $q$ resp.
Step 3: Filtering
- then filter the edges:
- remove all edges with weight less than some threshold
Step 4: Clusters
- let all connected components be clusters
Illustration
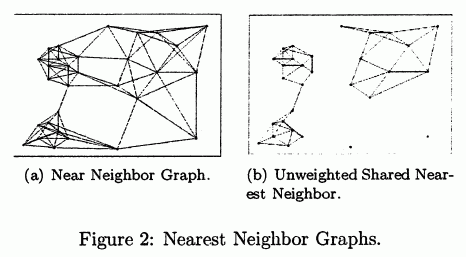
- (figure source: Ertöz2003)
- note that this procedure removed the noise
- and clusters are of uniform density: it breaks the links in the transition regions
Density
Usual density is not good:
- In the Euclidean space, the density is the number of points per unit volume
- but as dimensionality increases, the volume increases rapidly
- so unless the number of points increases exponentially with dimensionality, the density tends to 0
- Density-based algorithms (e.g. DBSCAN) will not work properly
Need different intuition of density
- can use a related concept from
- if $k$th nearest neighbor is close, then the region is most likely of high density
- so the distance to $k$th neighbor gives a measure of density of a point
- because of the Curse of Dimensionality, the approach is not good for Euclidean Distance, Cosine Similarity or others
- but we can use the SNN-Similarity to define density
SSN-based measures of density:
- sum of SSN similarities over all KNNs
- why sum an not just $k$th?
- to reduce random variation - which happens when we look only at one point
- to be consistent with the graph-based view of the problem
- of it can be the number of points within some radius - specified in terms of SNN distance
- like in DBSCAN, but with SSN distance
SSN Clustering Algorithm
SNN Clustering algorithm is a combination of
- Jarvis-Patrick algorithm and
- DBSCAN with SSN Similarity and SSN Density
Parameters
- $k$
- $\epsilon$
- $\text{min_pts} < k$
Steps:
- compute the similarity matrix
- sparsify the matrix by keeping only $k$ most similar neighbors for each data point
- construct the SSN graph (use the Jarvis-Patrick algo)
- find SSN density of each point $p$:
- in the KNN list of $p$ count $q$ s.t. $\text{sim}(p, q) \geqslant \epsilon$
- find the core points
- all points with SSN density greater than $\text{min_pts}$ are the core ones
- form clusters from the core points
- all non-core points not within $\epsilon$ from the core ones are discarded as noise
- align non-noise non-core points to clusters
Parameter tuning:
- $k$ controls granularity of clusters
- if $k$ is small, then it will find small and very tight clusters
- if $k$ is large, it’ll find big and well-separated clusters
Complexity
- The algorithm runs in $O(n^2)$ time
- can speed up with Kd-Trees or R-Trees
- alternatively, can use canopies
References
- Jarvis, Raymond A., and Edward A. Patrick. “Clustering using a similarity measure based on shared near neighbors.” (1973). [http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.474.2388&rep=rep1&type=pdf]
- See also: Houle, Michael E., et al. “Can shared-neighbor distances defeat the curse of dimensionality?.” 2010. [http://www.dbs.ifi.lmu.de/~zimek/publications/SSDBM2010/SNN-SSDBM2010-preprint.pdf]
Sources
- Ertöz, Levent, Michael Steinbach, and Vipin Kumar. “Finding clusters of different sizes, shapes, and densities in noisy, high dimensional data.” 2003. [http://static.msi.umn.edu/rreports/2003/73.pdf]