ML Wiki

Serializable Schedule

Serializable Schedule

Definitions

An action is

  • $r(X)$ - read database element $X$ or
  • $w(X)$ - write database element $X$
  • we abstract away from the actual values that are read/written, we are not interested in them

A transaction $T$ is a sequence of action

  • $r(A), r(B), w(A), w(B)$

A schedule is a sequence of actions that belong to different transactions

  • $r_1(A), w_1(A), r_2(A), w_2(A), r_1(B), w_1(B), r_2(B), w_2(B)$
  • $r_i(X)$ denotes that this action belongs to transaction $T_i$


Serializability

a serial schedule is a schedule in which transactions are executed consequently, not concurrently

  • e.g. first all actions of $T_1$ and then all actions of $T_2$
  • $\underbrace{r_1(A), w_1(A), r_1(B), w_1(B)}_{\text{all actions of $T_1$}}, \underbrace{r_2(A), w_2(A), r_2(B), w_2(B)}_{\text{all actions of $T_2$}}$

Serializable Schedule

  • a schedule is called serializable is there exists an equivalent serial schedule
  • even though we may execute actions concurrently, the effect is guaranteed to be the same as if it was run in isolation
  • $S_1 = r_1(A), w_1(A), r_2(A), w_2(A), r_1(B), w_1(B), r_2(B), w_2(B)$
  • $S_2 = r_1(A), w_1(A), r_1(B), w_1(B), r_2(A), w_2(A), r_2(B), w_2(B)$
  • $S_1 \equiv S_2$, $S_2$ is serial, so $S_1$ is serializable

Not serializable:

  • Write-Read conflict:
    • $r_1(A), w_1(A), r_2(A), w_2(A), r_2(B), w_2(B), r_1(B), w_1(B)$
    • write by $T_2$ happens before read by $T_1$, but $T_1$ started earlier
    • it's not equivalent to any serial schedule

We want to schedule our actions in such a way that the result is serializable

Conflict-Serializability

Serializability is very hard to achieve

two actions are in conflict if

  1. they belong to the same transaction
  2. both deal with the same element and one of the actions is a write

A schedule is conflict-serializable if

  • we can obtain a serial schedule by swapping actions that are not in conflict

Example:

  • $S_1 = r_1(A), w_1(A), \underbrace{r_2(A)}_\text{(1)}, \underbrace{w_2(A)}_\text{(2)}, \underbrace{r_1(B)}_\text{(3)}, \underbrace{w_1(B)}_\text{(4)}, r_2(B), w_2(B)$
    • $(1) + (2)$ are not in conflict with $(3) + (4)$: they use different DB items
    • can swap them and get a serial schedule
  • $S_2 = r_1(A), w_1(A), r_1(B), w_1(B), r_2(A), w_2(A), r_2(B), w_2(B)$
  • i.e. $S_1$ is conflict-serializable

NB:

  • you never can reorder actions of the same transaction
  • otherwise you may change the behavior of this transaction
  • what is more, by reordering actions within same transactions it's not possible to get something serial from not serializable schedule


Conflict-Serializability $\Rightarrow$ Serializability

but converse is not true

  • $S_1 = w_1(Y), w_2(Y), w_1(X), w_3(X)$
  • $S_2 = w_1(Y), w_1(X), w_2(X), w_3(X)$
  • $S_1 \equiv S_2$: in $Y$ there's a value written by $T_2$, and in $X$ the value written by $T_3$
  • but S_1 is not Conflict-Serializable, but Serializable: we cannot swap $w_2(X)$ and $w_1(X)$

Precedence Graph

There is an algorithm that checks if a schedule is conflict-serializable

construct a precedence graph:

  • suppose you have a schedule $S$ with several transactions
  • create a node for each transaction
  • connect $T_i$ with $T_j$ if
    • there $\exists$ actions $a_i \in T_i, a_j \in T_j$ s.t.
    • $a_i$ precedes $a_j$ and
    • $a_i$ are in conflict $a_j$ and

Example 1:

  • $S_1 = {\color{red}{r_2(A)}}, {\color{blue}{r_1(B)}}, w_2(A), r_3(A), w_1(B), {\color{red}{w_3(A)}}, r_2(B), {\color{blue}{w_2(B)}}$
  • pred-graph-1.png

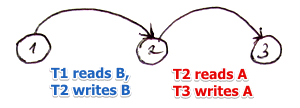
Example 2:

  • $S_2 = w_1(Y), w_2(y), w_2(X), w_1(X), w_3(X)$
  • pred-graph-2.png


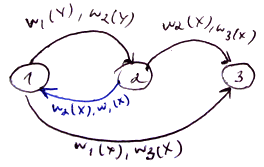
Thm If the precedence graph $G$ of a schedule $S$ is a DAG then

  • $S$ is conflict-serializable
  • otherwise it's not

Suppose we have a cycle $T_1 \to ... \to T_n \to T_1$ in $G$

  • it means there $\exists$ action $a_1 \in T_1$ on some database item $X$ that follows $a'_n \in T_n$ on the same $X$
    • we cannot move $a_1$ by conflict-free swapping to the front
    • i.e. cannot put $a_1$ before all actions of $T_n$
  • there also $\exists$ $a_n$ that follows some action $a'_1 \in T_1$
    • but we cannot move $a_n$ either because of some action $a_{n-1} \in T_{n-1}$
  • i.e. we cannot have a conflict-serializable schedule


But if $G$ is a DAG, we can obtain an equivalent conflict-serializable schedule by Topological Ordering

  • if there are no cycles in $G$ then
    • there $\exists$ a transaction $T_A$ that has no incoming edges in $G$
    • otherwise there would be a cycle
  • let $a_1$ be the first action of $T_A$
  • can move $a_1$ by conflict-free swapping to the front
    • since $T_A$ has no incoming edges, there are no actions that conflict with $a_2$
  • let $a_2$ be the second action of $T_A$
    • also can move it to the front
  • repeat for all actions $a_i \in T_A$
  • we end up with the following schedule:
    • $S' = \underbrace{a_1, a_2, ..., a_k}_{\text{all actions $\in T_A$}}, \underbrace{b_1, c_1, ..., z_p}_{\text{all actions $\not \in T_A$}}$
  • now remove all actions of $T_A$, let $G$ be the precedence graph of this schedule and repeat

If there are 2 or more nodes with no incoming edges, just pick one of them

  • the result in any case will be serial
  • only the order may be different

$\square$

Schedulers

A Scheduler is a component of Transaction Manager that schedules read/write requests.

The following schedulers produce Conflict-Serializable Schedules:

Sources

Retrieved from "http://mlwiki.org/index.php?title=Serializable_Schedule&oldid=252"