Space Orthogonality
Contents
Space Orthogonality
Two vectors (sub)spaces can also be orthogonal
Consider two subspaces $S$ and $T$
- $S \; \bot \; T$ means that $\forall \mathbf s \in S, \forall \mathbf t \in T: \mathbf s \; \bot \; \mathbf t$
- i.e. if every vector in $T$ is orthogonal to every vector in $S$, then $S$ and $T$ are orthogonal
Examples
Example 1
Suppose you have two spaces: a wall and a floor. Are they orthogonal?
-
- take one vector from the wall that is 45° to one of the axis. It's not orthogonal to the floor! it's 45°
- also, there are vectors that belong to both subspaces (and not just the origin!) - these vectors are not orthogonal
So, if two spaces intersect in more than just the zero-vector, then they cannot be orthogonal
Example 2
Two subspaces that meet in $\mathbf 0$ can be orthogonal
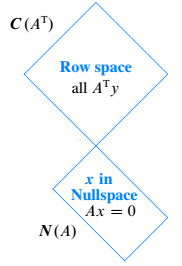
Row space and Nullspace
Row space $C(A^T)$ and nullspace $N(A)$ are orthogonal.
why?
Let's consider only rows from $A$
- $\mathbf x \in N(A) \Rightarrow A \mathbf x = \mathbf 0$
- $\begin{bmatrix}
— (\text{row 1}) \,— \\ — (\text{row 2}) \,— \\
\vdots \\
— (\text{row $n$}) \,— \end{bmatrix} \cdot \mathbf x = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix}$
- or $\begin{bmatrix}
(\text{row 1})^T \mathbf x = 0 \\ (\text{row 2})^T \mathbf x = 0 \\
\vdots \\
(\text{row $n$})^T \mathbf x = 0 \\ \end{bmatrix}$
- so $\mathbf x$ is orthogonal to all rows in $A$
what else is in the row space? linear combinations of rows of $A$
- $c_1 \cdot \text{row 1} + \ ... \ + c_n \cdot \text{row $n$}$ what if we multiply it by $\mathbf x$?
- $(c_1 \cdot \text{row 1} + \ ... \ + c_n \cdot \text{row $n$})^T \mathbf x = (c_1 \cdot \text{row 1})^T \mathbf x + \ ... \ + (c_n \cdot \text{row $n$})^T \mathbf x = c_1 \cdot \underbrace{(\text{row 1})^T \mathbf x}_{0} + \ ... \ + c_n \cdot \underbrace{(\text{row $n$})^T \mathbf x}_{0} = 0$
Column Space and Left Nullspace
They are orthogonal for exactly the same reason
- just transpose $A$ and go through the same argument as for row space and nullspace
Orthogonal Compliments
$N(A) \; \bot \; C(A^T)$ and $\text{dim} N(A) + \text{dim} C(A^T) = n$
- they add up to the whole space
- so they are orthogonal compliments in $\mathbb R^n$