Genetic Process Miner
This is an algorithm from the family of Genetic Algorithms for mining business processes
- it’s much more resilient to noise
- allows for incremental improvement
- can be combined with other approaches
Overview

- first we create the initial population
- can just randomly create some Petri Nets, randomly adding places
- or by applying Alpha Algorithm or Region-Based Process Miner
- at each step we compute fitness for all the instances of a population
- elitism - process of keeping the best ones
- then all “survived” instances are considered as “parents”
- cross-over - process of combining different petri nets (these petri-nets are already good solutions)
- mutation adding some random changes for diversifying
Cross-Over
Cross-over
- a process of producing a “child” by two parental instances
- selecting parents
- completely at random
- using fitness to quicker converge to optima
- note that we should not always select only “the best” - we need diversity
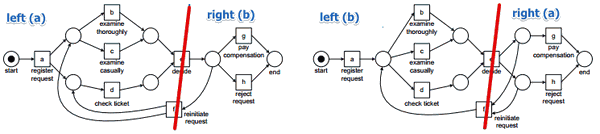
How to create a petri net from two other petri nets?
- suppose we have two parental petri nets:
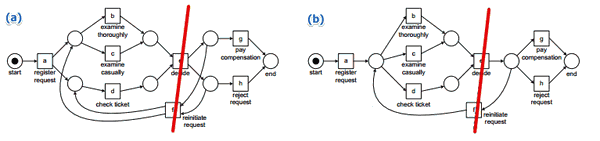
- we may find some ‘‘minimal cut’’, cut the parents and make children from then
- minimal cut is the minimal number of transitions to remove s.t. the net becomes completely disconnected
- the same as in the Graph Theory: Minimal Cut
- in this example:
- can cut in $(e, f)$ because in both cases
- from $e$ it goes to $g,h$ and on the left you have $a,b,c,d$
- so it’s ideal
- we take $(e, f)$ out and get two disconnected components
- combine left and right parts of the petri nets to form children
Mutation
Examples of mutations:
- remove or add a place
- add an arc
Parameters
So there are quite a few parameters that we have to provide:
- objective function we want to optimize (below)
- the way we do the cross-over
- how do you select parents?
- the way we do the mutations
- elitism - top 10%, certain threshold, etc
- how large the population should be
- how many generations you’ll run before termination
- when we kill some instances?
Change one parameter
- $\Rightarrow$ different solution in the end
Also
- a lot of randomness is involved
- it may be computationally expensive
Cost Function: Fitness
Trace Level Fitness
Define ‘‘trace-level fitness’’ as:
- $\text{fitness}(\sigma, N) = \cfrac{1}{2} \left( 1 - \cfrac{m}{c} \right) + \cfrac{1}{2} \left( 1 - \cfrac{r}{p} \right)$
- $m$ - # of missing tokens
- $c$ - # of consumed tokens
- $r$ - # of tokens left over when something reaches the output place
- $p$ - # of produced tokens
Example 1
Consider this example:
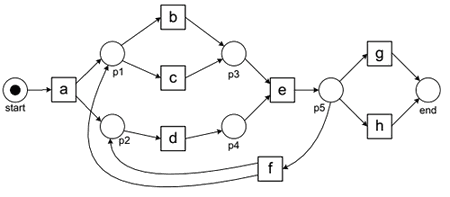
- logtrace: $\sigma_1 = \langle abeg \rangle$
- $m = 0, c = 0, r = 0, p = 1$
- $p = 1$ because there’s a token in the input place
- $a$ fires - it generates 2 tokens
- $p \leftarrow p + 2 = 3$
- $c \leftarrow c + 1 = 1$
- $b$ fires, produces one token, consumes one token
- $p \leftarrow p + 1 = 4$
- $c \leftarrow c + 1 = 2$
- $e$ needs to fire
- but it cannot: one token is missing, so we add it and fire $e$
- $p \leftarrow p + 1 = 5$
- $c \leftarrow c + 2 = 4$
- $m \leftarrow m + 1 = 1$
- $g$ fires and we’re done
- $p \leftarrow p + 1 = 6$
- $c \leftarrow c + 1 = 5$
- but there’s one remaining token that was left over after firing $a$
- $r \leftarrow r + 1 = 1$
- and finally we remove one token from the output place
- $c \leftarrow c + 1 = 6$
- $\text{fitness}(\sigma_1, N_1) = \cfrac{1}{2} \left( 1 - \cfrac{1}{6} \right) + \cfrac{1}{2} \left( 1 - \cfrac{1}{6} \right) = \cfrac{5}{6}$
Example 2

- logtrace: $\sigma_2 = \langle adceh \rangle$
- $p = 1, c = 0, m = 0, r = 0$
- $a$ fires, produces 1, consumes 1
- $p \leftarrow 2, c \leftarrow 1$
- $d$ needs to fire
- but there’s no token in the place before $d$, so we need to put it there
- $m \leftarrow 1$
- $d$ fires: $p \leftarrow 3, c \leftarrow 2$
- $c$ fires
- $p \leftarrow 4, c \leftarrow 3$
- note that $c$ and $d$ were executed in order different from the order that the model can produce
- $e$ fires
- $p \leftarrow 5, c \leftarrow 4$
- $h$ fires
- $p \leftarrow 6, c \leftarrow 5$
- we’re done
- one token is left: $r \leftarrow 1$
- taking the last token from $c$: $c \leftarrow 6$
- $\text{fitness}(\sigma_2, N_2) = \cfrac{1}{2} \left( 1 - \cfrac{1}{6} \right) + \cfrac{1}{2} \left( 1 - \cfrac{1}{6} \right) = \cfrac{5}{6}$
Log Level Fitness
Log-level fitness is
- fitness, calculated for each trace and aggregated
- $\text{fitness}(L, N) = \cfrac{1}{2} \left( 1 - \cfrac{\sum_{\sigma \in L} L(\sigma) \times m_{N, \sigma}}{\sum_{\sigma \in L} L(\sigma) \times c_{N, \sigma} } \right)
- \cfrac{1}{2} \left( 1 - \cfrac{\sum_{\sigma \in L} L(\sigma) \times r_{N, \sigma}}{\sum_{\sigma \in L} L(\sigma) \times p_{N, \sigma} } \right)$
- $L(\sigma)$ how many times the trace $\sigma$ occurred in log $L$
Links
- http://www.processmining.org/blogs/pub2006/genetic_process_mining