Region-Based Process Miner
This is a state-based approach to Process Mining
- as opposed to the Alpha Algorithm, which is footprint-based
Motivation
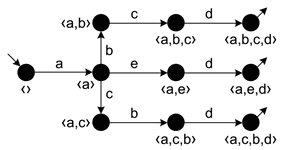
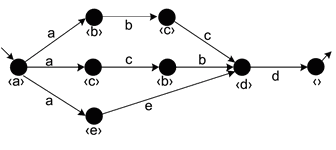
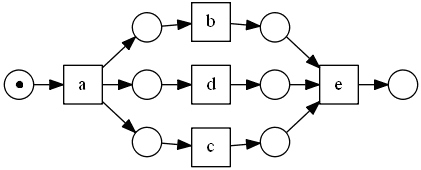
Consider the following Petri Net:
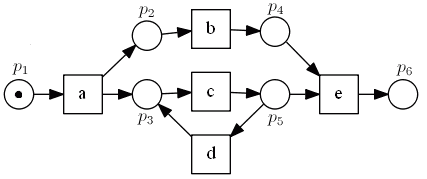
- here’s its Reachability Graph:
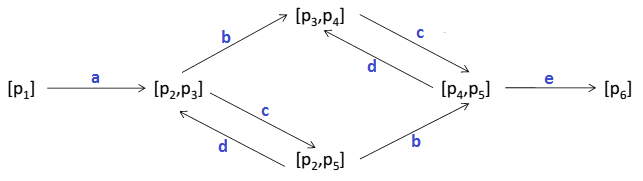
Suppose that for each place $p_i$ we identify the set of nodes $R_i$ in the graph (i.e. the set of markings) where $p_i$ has a token:
- $p_1: R_1 \equiv {[p_1]}$
- $p_2: R_2 \equiv {[p_2, p_3], [p_2, p_5]}$
- $p_3: R_3 \equiv {[p_2, p_3], [p_3, p_4]}$
- $p_4: R_4 \equiv {[p_3, p_4], [p_4, p_5]}$
- $p_5: R_5 \equiv {[p_2, p_5], [p_4, p_5]}$
- $p_6: R_6 \equiv {[p_6]}$
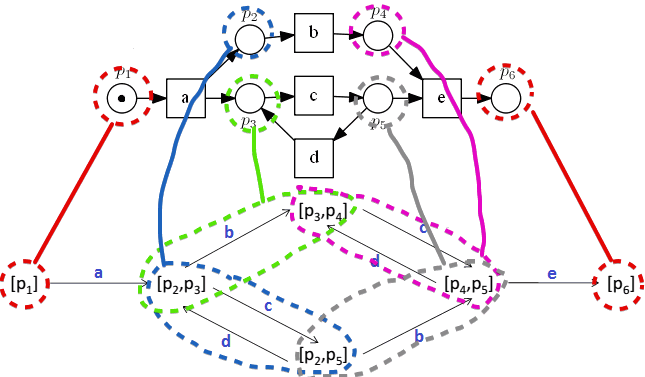
If we look carefully, we see that:
- for place $p_2$ in the region $R_2$
- $a$ brings us into the region $R_2$ and $b$ takes us out this region
- meanwhile transitions $c$ and $d$ are always either completely inside $R_2$ or completely outside $R_2$
- for $p_4$ in $R_4$
- $b$ brings in, $e$ takes out
- again $c$ and $d$ do not cross the boundaries of $R_4$
We can notice the same patterns for all the regions
- there are transitions that bring in and there are transitions that take out from the region
- and such transitions are connected with a place
- there also are transitions that keep us inside the region
Transition System
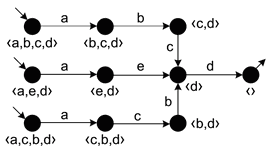
But usually we do not know where are the tokens, we may know only that there are some states:
- this is called a ‘‘transition system’’: we know the states, but don’t know which places have tokens
- yet we still can use this idea to recognize the structural properties
- and try to reconstruct the original model
How?
- create a transition system from logs
- find groups of nodes – ‘‘regions’’ – in the transition system
- add places to capture the behavior
Creating a Transition System
How to create a transition system?
- solution: an educated guess.
A state may depend on:
- (1) actions taken so far, and the number of times they were executed
- (2) actions we will do in the future
- (1) and (2)
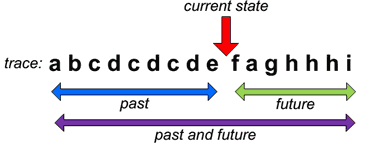
So there are many way of “learning” the transition system
- this is about guessing and trial and errors
- and a little bit of knowledge of the domain is also helpful to choose the right abstraction
Past Without Abstraction
Sometimes also called “prefix automaton”
- to define the state we look at what we’ve seen so far
- we don’t make any abstractions:
- i.e. the sequence $\langle a, b \rangle \ne \langle b, a \rangle $
Algo:
- at the beginning the path-so-far is empty
- after $a$ fires, you add it to the sequences of the seen events
For log $L = [abcd, acbd, acd]$ we have:
Downsides:
- not generalizing at all
- end up with one path for each trace
- want to “abstract” from this: want states to join after a while
Future Without Abstraction
Based on things that you will see in the logs
- some states can be merged with this approach
For log $L = [abcd, acbd, acd]$ we have:
Better
- we see that it can generalize a bit
- i.e. recognize the same suffixes of different trances and join them
Past with Multiset Abstraction
Now we add some abstraction:
- order in which we have seen the traces in not important anymore
- two states are considered to be the same if all activities we’ve seen so far fired equal number of times
- i.e. the traces-so-far form a multiset
- and $[a, b, c] \equiv [a, c, b]$
- this works well for Petri Nets as long as there are no transitions with the same name
For log $L = [abcd, acbd, acd]$ we have:
Only Last Event Matters
Another abstraction:
- we keep only one most recently seen event
- so it’s a Markov Chain with memory of 1
- and what you can do next depends only on what you’ve just seen
For log $L = [abcd, acbd, acd]$ we have:
Only Next Event Matters
Analogously,
- but here we care only about the next event
For log $L = [abcd, acbd, acd]$ we have:
Note:
- we see that firing $a$ can bring us to 3 different states
-
not deterministic - you’ll never see such thing in a Reachability Graph of a Petri Net - most likely wrong abstraction
Examples
Consider this log: $L_2 = [abcd, abcdce, acbe, acdbce, acbdce]$
- for each trace in the log we try build a branch in the transition system
Past with Set Abstraction
$L_2 = [abcd, abcdce, acbe, acdbce, acbdce]$
| $abcd$ |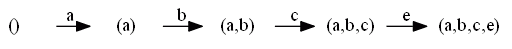 
|| $abcd$ | 
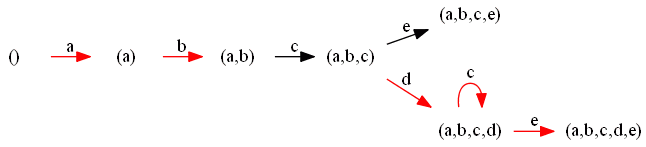|| $acbe$ | 
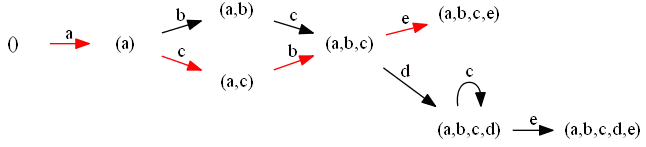|| $acdbce$ | 
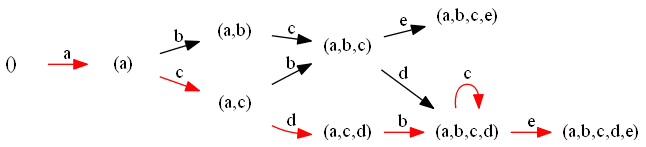|| $acbdce$ | 
|
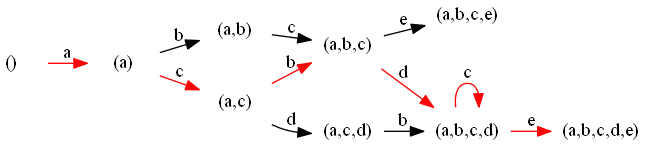But because of the set abstraction we must have lost some information:
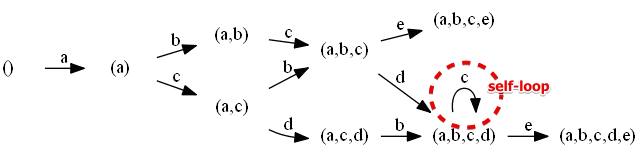
- there’s a self-loop that keeps us in the same state
- so there may be something wrong - we must make sure such things are expected
- in this log it’s clear that it’s not the case (we never see anything like $…cc…$, $…ccc…$, etc)
- so it allows too much behavior that we don’t see in the logs
Conclusions
We see that it may be very hard to select the right way of constructing the transition system
- we need to try and see
- select an abstraction
- construct the transition system from it
- try to extract a petri net
- evaluate quality
- see if it makes sense
- some domain knowledge is always helpful
Theory of Regions
Regions
a region $R$ is a set of states of a transition system $T$ s.t.
- if a transition $t$ exits $R$, then all arcs labeled with $t$ must exist $R$
- if $t$ enters $R$, then all arcs labeled with $t$ must enter
- all other transitions $t$ must not cross the boundaries of $R$
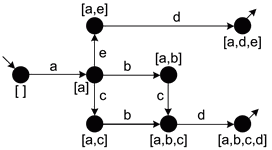
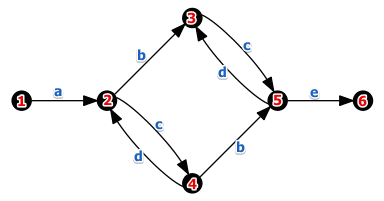
Example 1
Consider this transition system:
Identify the following regions:
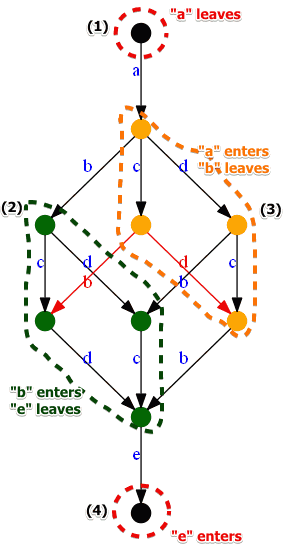
- (1): noting enters, only $a$ leaves: $a$ is connected to the input place $i$
- (2): $b$ enters, $e$ leaves, others don’t cross the boundary: collect $b$ and $e$ via a place
- (3): $a$ enters, $b$ leaves: connect them via a place
- (4): connect $e$ to the output place $o$
- so we have:
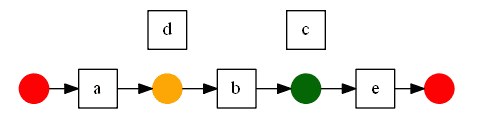
Next, find two mode regions:
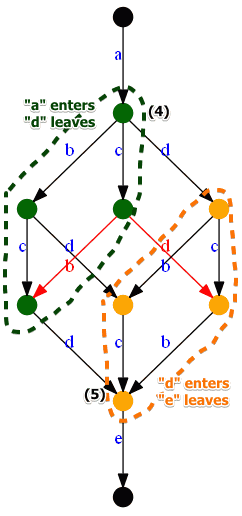
- (5): $a$ enters, $d$ leaves, connect them
- (6): $d$ enters, $e$ leaves, connect them
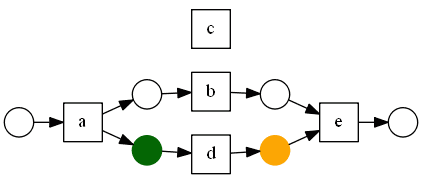
And finally:
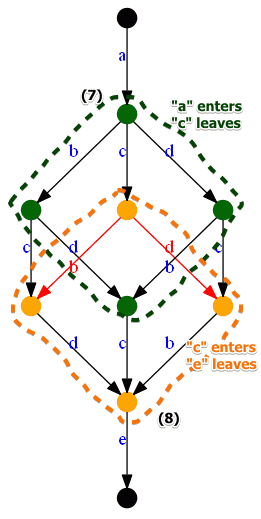
- (7) $a$ enters, $c$ leaves
- (8) $c$ enters, $e$ leaves
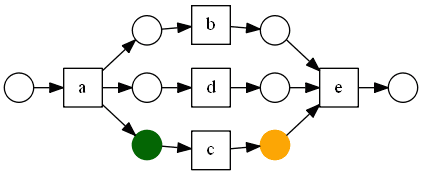
So the discovered network is:
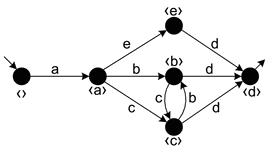
Examples of not regions:
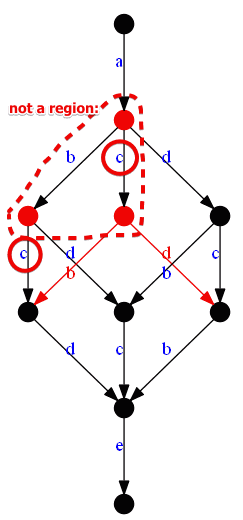
- this is not a region: $c$ is both inside the region and exists it
- the same for $b$ and $d$
- it it corresponded to a place, it would be a very strange place:
- sometimes when a token is in $c$ it cold fire, but it would keep the token
- and sometimes it would consume the token
Example 2
For example, consider the following transition system:
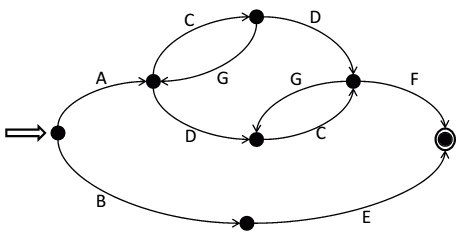
- we see that there are 7 transitions: $A,B,C,D,E,F,G$
how to connect them?
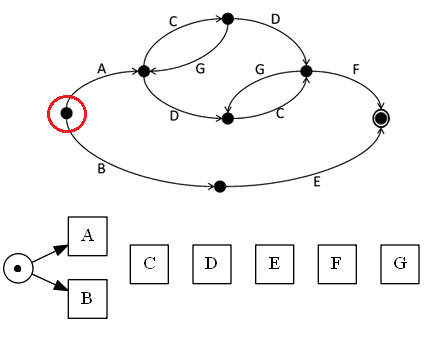
- nothing enters this region
- transitions $A$ and $B$ leave the region
- so we must connect the input place with these transitions
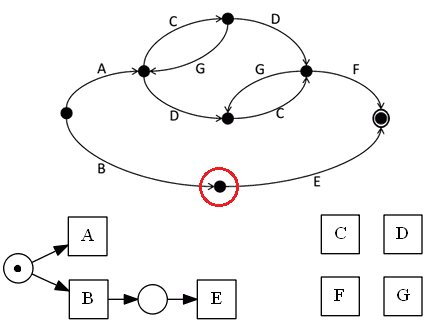
- for this region, $B$ enters, $E$ leaves
- so we connect $B$ and $E$ with a place
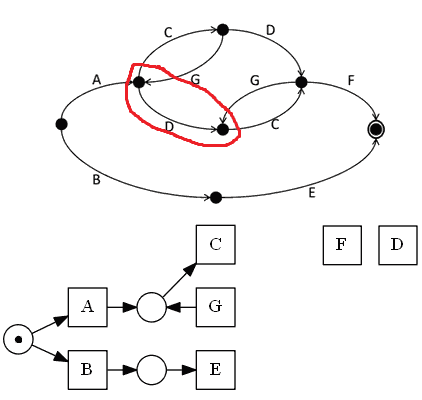
- $A$ and $D$ enter; $C$ leave
- so we add one place, and connect $A$ and $D$ to it, and the place to $C$
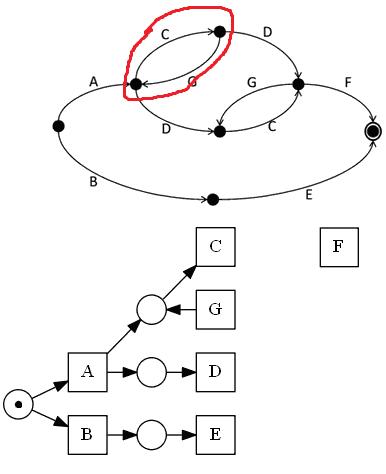
- analogously we connect $A$ and $D$ via a place
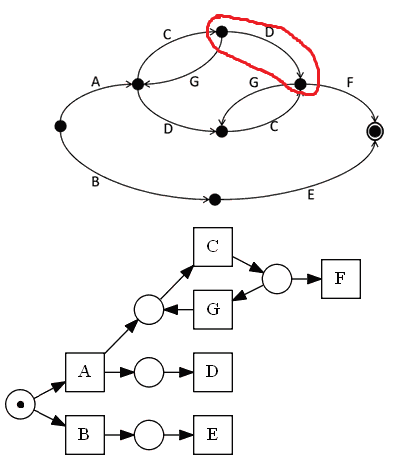
- $C$ enters the region, $G$ and $F$ leave
- we connect $C$ to a place, and the place to $G$ and $F$
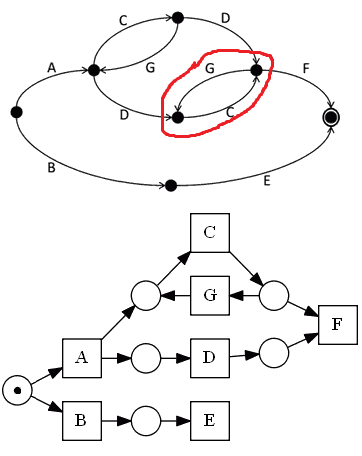
- connect $D$ and $F$
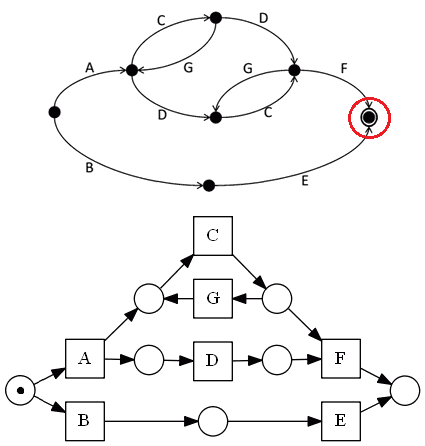
- and finally, $F$ and $E$ are connected to the final place
Minimal Regions
It’s important to have regions as minimal as possible
- otherwise a region may correspond to several places
Regions
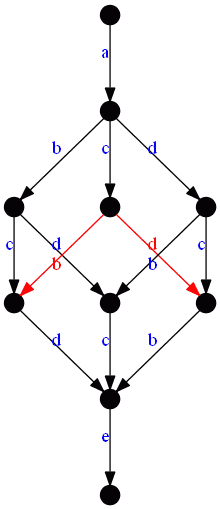
- all nodes together form a region
- all nodes except for the first and last one - also form a region
- enter by doing $a$, exit by doing $e$
- but we want to find minimal ‘‘non-trivial’’ regions
'’Trivial’’ regions
- empty region (nothing takes in, nothing takes out - a region as well)
- all nodes together
All other regions:
- combination of two or more minimal regions
Properties
Let $S$ be a set of all states of a transition system
- trivial regions: $S$, $\varnothing$
- compliments: if $R$ is a region, then $S - R$ is also a region
- but the complimentary region is not necessarily minimal
Basic Algorithm
Compute $S^*$ - the set of all minimal regions
- for each $R \in S^*$ generate a place:
- add arcs between
- post-region of $R$ (transitions that leave $R$) - output for that place
- pre-region of $R$ (transitions that enter $R$) - input for that place
- add a token to each place that correspond to initial regions
The result - is the minimal saturated net
Limits
Loops of Length 1
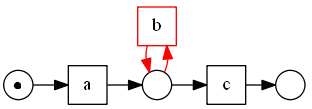
- in this example $b$ can fire $\infty$ number of times
- but you cannot detect it - $b$ cannot be a pre-region and a post-region at the same time
- there are mechanisms to overcome this problem - like in the $\alpha^+$ algorithm
Susceptibility to Noise
Suppose by mistake instead of $b$ you have $bb$
- that can completely spoil your logs
- so first we need to pre-process logs to make sure there are no noise
- or we can weaker the “region” condition - assume that it’s enough to have transitions completely inside or outside only in 99% of cases
- and allow crossing in 1%