Machine Learning Diagnosis
Suppose you created a model, but when you tested it, you found that it makes large errors
What should you try?
- Get more training examples
- Try smaller set of features
- Try getting additional features
-
Try adding polynomial features (beware of Overfitting ) - Try increasing regularization parameter $\lambda$ - Try decreasing $\lambda $
'’Diagnosis’’ - a test that you can run to gain insights what is working with the learning algorithms and what is not, and gain guidance as how to improve the performance.
Evaluating a Hypothesis
To test if we overfit, we can perform Cross-Validation:
- train the model on the training set
- check the model on the test set
Diagnosing Bias vs Variance
the main sources of problems are
- high bias (underfit)
- high variance (Overfitting)
Fitting Polynomial
How to distinguish between them and say which one of them we experience?
- Suppose we want to fit parameter $d$ - what degree of polynomial to use (see here)
- with $d = 1$ we underfit
- with $d = 2$ we are just right
- with $d = 4$ we overfit
We can plot the cost function errors vs degree of polynomial $d$ for
- the training set $J_{\text{train}}(\theta)$
- the cross-validation (or test) set $J_{\text{cv}}(\theta)$
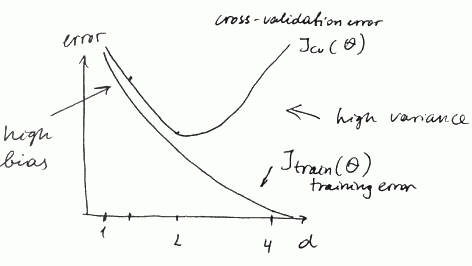
in case of bias (underfit) we have
- both $J_{\text{train}}(\theta)$ and $J_{\text{cv}}(\theta)$ are high
- and $J_{\text{train}}(\theta) \approx J_{\text{cv}}(\theta)$
in case of variance (overfit)
- $J_{\text{train}}(\theta)$ is low, $but J_{\text{cv}}(\theta)$ is high
- and $J_{\text{cv}}(\theta) \gg J_{\text{train}}(\theta)$ (much greater)
Fitting Regularization Parameter
- When we try to find the best Regularization parameter for a hypothesis we get similar curves:
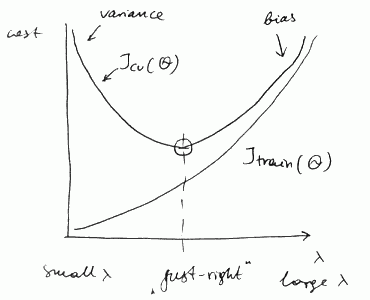
- with small $\lambda$ we have high variance
- with large $\lambda$ we have high bias
Learning Curves
Learning Curves is a technique that is used to
- sanity-check our algorithm or
- improve performance
- diagnose high bias (underfit)
- diagnose high variance (overfit)
What To Do Next?
So, depending on what kind of problem we have, we should decide what to do next
To fix high variance:
- Get more training examples
- Try smaller set of features
- Try decreasing regularization parameter $\lambda$
To fix high bias:
- Try getting additional features
-
Try adding polynomial features (beware of Overfitting ) - Try increasing regularization parameter $\lambda$