Ordinary Least Squares Regression
- This is a technique for computing coefficients for Multivariate Linear Regression.
- the solution is obtained via minimizing the squared error, therefore it’s called ‘‘Linear Least Squares’’
- two solutions: Normal Equation and Gradient Descent
- this is the the typical way of solving the Multivariate Linear Regression, therefore it’s often called ‘'’OLS Regression’’’
Regression Problem
Suppose we have
- $m$ training examples $(\mathbf x_i, y_i)$
- $n$ features, $\mathbf x_i = \big[x_{i1}, \ … \ , x_{in} \big]^T \in \mathbb{R}^n$
- We can put all such $\mathbf x_i$ as rows of a matrix $X$ (sometimes called a ‘‘design matrix’’)
- $X = \begin{bmatrix}
- \ \mathbf x_1^T - \ \vdots \
- \ \mathbf x_m^T - \ \end{bmatrix} = \begin{bmatrix} x_{11} & \cdots & x_{1n} \ & \ddots & \ x_{m1} & \cdots & x_{mn} \ \end{bmatrix}$
- the observed values: $\mathbf y = \begin{bmatrix} y_1 \ \vdots \ y_m \end{bmatrix} \in \mathbb{R}^{m}$
- Thus, we expressed our problem in the matrix form: $X \mathbf w = \mathbf y$
- Note that there’s usually additional feature $x_{i0} = 1$ - the slope,
- so $\mathbf x_i \in \mathbb{R}^{n+1}$ and $X = \begin{bmatrix}
- \ \mathbf x_1^T - \
- \ \mathbf x_2^T - \ \vdots \
- \ \mathbf x_m^T - \ \end{bmatrix} = \begin{bmatrix} x_{10} & x_{11} & \cdots & x_{1n} \ x_{20} & x_{21} & \cdots & x_{2n} \ & & \ddots & \ x_{m0} & x_{m1} & \cdots & x_{mn} \ \end{bmatrix} \in \mathbb R^{m \times n + 1}$
Thus we have a system
- $X \mathbf w = \mathbf y$
- how do we solve it, and if there’s no solution, how do we find the best possible $\mathbf w$?
Least Squares
Normal Equation
There’s no solution to the system, so we try to fit the data as good as possible
- Let $\mathbf w$ be the best fit solution to $X \mathbf w \approx \mathbf y$
- we’ll try to minimize the error $\mathbf e = \mathbf y - X \mathbf w$ (also called residuals)
- we take the square of this error, so the objective is
-
$J(\mathbf w) = | \mathbf e |^2 = | \mathbf y - X \mathbf w |^2$
The solution:
- $\mathbf w = (X^T X)^{-1} X^T \mathbf y = X^+ \mathbf y$
- where $X^+ = (X^T X)^{-1} X^T$ is the Pseudoinverse of $X$
From the Linear Algebra point of view:
- we need to solve $X \mathbf w = \mathbf y$
- if $\mathbf y \not \in C(X)$ (Column Space) then there’s no solution
-
How to solve it approximately? Project on $C(A)$ - again, it gives us the Normal Equation: $X^T X \mathbf w = X^T \mathbf y$
Gradient Descent
Alternatively, we can use Gradient Descent:
-
objective is $J(\mathbf w) = | \mathbf y - X \mathbf w |^2$ - the derivative w.r.t. $\mathbf w$ is $\cfrac{\partial J(\mathbf w)}{\partial \mathbf w} = 2 X^T X \mathbf w - 2 X^T \mathbf y$ - so the update rule is $\mathbf w \leftarrow \mathbf w - \alpha 2 (X^T X \mathbf w - X^T \mathbf y)$
- where $\alpha$ is the learning rate
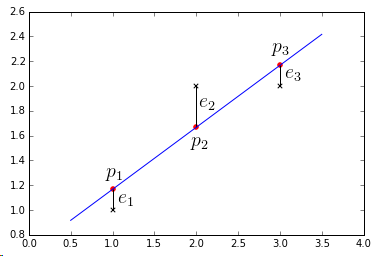
Example
Suppose we have the following dataset:
- ${\cal D} = { (1,1), (2,2), (3,2) }$
- the matrix form is $\begin{bmatrix}
1 & 1\
1 & 2\
1 & 3
\end{bmatrix} \begin{bmatrix} w_0 \ w_1 \end{bmatrix} = \begin{bmatrix} 1 \ 2 \ 2 \end{bmatrix}$ - no line goes through these points at once
- so we solve $X^T X \mathbf{\hat w} = X^T \mathbf y$
- $\begin{bmatrix}
1 & 1 & 1 \
1 & 2 & 3 \
\end{bmatrix} \begin{bmatrix}
1 & 1\
1 & 2\
1 & 3
\end{bmatrix} = \begin{bmatrix} 3 & 6\ 6 & 14
\end{bmatrix}$ - this system is invertible, so we solve it and get $\hat w_0 = 2/3, \hat w_1 = 1/2$
- thus the best line is $h(t) = w_0 + w_1 t = 2/3 + 1/2 t$
Normal Equation vs Gradient Descent
- need to choose learning rate $\alpha$
- need to do many iterations
- works well with large $n$
- don’t need to choose $\alpha$
- don’t need to iterate - computed in one step
- slow if $n$ is large $(n \geqslant 10^4)$
- need to compute $(X^T X)^{-1}$ - very slow
- if $(X^T X)$ is not-invertible - we have problems
See Also
Sources
- Linear Algebra MIT 18.06 (OCW)
- Machine Learning (coursera)
- Seminar Hot Topics in Information Management IMSEM (TUB)
- http://en.wikipedia.org/wiki/Linear_least_squares_%28mathematics%29