ML Wiki

Cost-Based Plan Selection exercises

• Wiki Articles:
  • Physical Operators (databases)
  • Physical Query Plan Optimization
  • Join Ordering
  • Query Result Size Estimation
• exercises handout: [1]
• solutions: [2]

Exercise 2

Suppose we have 3 relations

• $E$(eid: int, did: int, sal: int, hobby: char(20))
• $D$(did: int, dname: char(20), floor:int, phone: char(10))
• $F$(did: int, budget: int, sales: int, expenses: int)

Statistics and parameters:

• 2048 bytes per block, 10 memory buffers are available
• record from $E$ is 35 bytes long, from $D$ - 40 bytes, from $F$ - 15 bytes
• indexes:
  • unclustered B-Trees on $E$.did and $D$.floor
  • clustered B-Trees on $E$.sal, $D$.did and $F$.did
• statistics:
  • $E$'s salaries are distributed uniformly within range [10 000, 60 000]
  • in $E$ there are 200 distinct hobbies - $V(E, \text{hobby}) = 200$
  • there are 2 floors
  • $T(E) = 50000, T(D) = 5000$

Select the Physical Query Plan based on I/O Cost

Query

$ \pi_{

 \begin{subarray}{l}
   \text{D.dname} \\
   \text{F.budget} \\
 \end{subarray}

} \big[ \sigma_{

 \begin{subarray}{l}
   \text{E.hobby = 'yodeling' } \land \\
   \text{E.sal } \geqslant 59000  \\
 \end{subarray}

} (E) \Join \sigma_\text{D.dloor = 1} (D) \Join F \big] $

• logical query plan:
• 

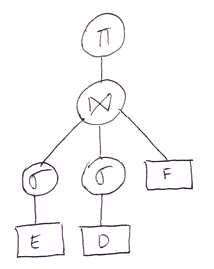
Solution Plan

• calculate number of blocks for each relations
• find the best plan for each selection individually
  • Estimate result size for each
• find the optimal Join Ordering

Some calculations

• for $E$ we can store $\left\lfloor \cfrac{2048}{35} \right\rfloor = 58$ tuples in one block
• $B(E) = \left\lceil \cfrac{50k}{58} \right\rceil = 863$
• for $D$ can store $\left\lfloor \cfrac{2048}{40} \right\rfloor = 51$ tuples in one block
• $B(D) = \left\lceil \cfrac{5k}{51} \right\rceil = 99$
• for $F$ can store $\left\lfloor \cfrac{2048}{15} \right\rfloor = 136$ tuples in one block
• $B(F) = \left\lceil \cfrac{5k}{136} \right\rceil = 37$

Selection 1

$s_R = \sigma_{

 \begin{subarray}{l}
   \text{E.hobby = 'yodeling' } \land \\
   \text{E.sal} \geqslant 59k  \\
 \end{subarray}

} (E)$

• same as
• $e_E \equiv \sigma_\text{E.hobby = 'yodeling'}\sigma_{\text{E.sal} \geqslant 59k} (E)$

Selectivity

• $\text{sel}_{\text{E.sal} \geqslant 59k}(E) \approx \cfrac{60k-59k}{60k-10k} \approx \cfrac{1}{50}$
• $\text{sel}_{\text{E.hobby = 'yodeling'}}(E) \approx \cfrac{1}{200}$ (200 distinct hobbies)
• it therefore produces $T(E) \times \text{sel}_{\text{E.sal} \geqslant 59k}(E) \times \text{sel}_{\text{E.hobby = 'yodeling'}}(E) = \cfrac{T(E)}{50 \times 200} = 5$ tuples
• output can be stored in one block

ways to get the results:

1. use the clustered B-Tree on $\text{E.sal}$
   • index scan: get records that satisfy $\text{E.sal} \geqslant 59k$
   • while doing index scan, filter records with $\text{E.hobby = 'yodeling'}$
   • cost:
     • number of accessed tuples $\text{sel}_{\text{E.sal} \geqslant 59k}(E) \times T(E) = 1000$
     • index is clustered - no need to follow each pointer (index scan)
     • $\left\lceil \cfrac{1000}{58} \right\rceil = 18$ Blocks (and therefore 18 I/Os)
2. don't use the index
   • table scan on $E$
   • filter records that satisfy both criteria
   • cost: $B(E) = 863$

Note:

• filtering on hobby does not require additional I/Os (it's pipelined)
• here we don't take index lookup cost into account (however it can be 2-3 I/Os per lookup - can increase the total I/O cost significantly if index is not clustered)

The first approach (index scan) yields better results - we will use it.

Selection 2

$s_D = \sigma_\text{D.dloor = 1}(D)$

• selectivity: $\text{sel}_\text{D.dloor = 1} (D) = \cfrac{T(D)}{V(D, \text{floor})} = \cfrac{5000}{2} = 2500$
• output can be stored in 49 blocks

ways to get the result

1. use unclustered B-Tree
   • 2500 I/Os since the index is not clustered, need to follow each pointer
2. full table scan
   • 99 I/Os

Join Ordering

Result so far:

• 
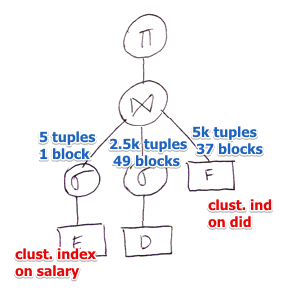
• now need to determine in what order we will execute the joins

Pair-wise comparison:

• $s_E \Join s_D$
• $s_E \Join F$
• $s_D \Join F$

Note

• we need to take into account the possibility of Pipelining
• no index on intermediate results $s_E$ and $s_D$

$s_E \Join s_D$

• one-pass join
  • cost: $B(s_E) + B(s_D) = 1 + 50 = 51$
• can't apply index-based join
• other algorithms are always worse than these two
• result: 5 tuples (1 block)

$s_E \Join F$

• we use 1 buffer for selection of $E$ and pipeline the output to this join
  • i.e. we have 9 buffers at our disposal
• can apply one-pass join
  • cost: $B(s_E) + B(F) = 1 + 37 = 38$
  • here we also ignore the output cost
  • note that if these two relations had no attributes in common, it would result in a Cartesian product, and the output would be huge. Here for simplicity we do not consider the output cost, only the I/O cost of performing the operation
• also can apply index-join (have a clustered BTree on F.did)
  • cost: 1 + 5
  • load $s_E$ into memory and for each tuple there look up a record block
• index-join is better
• result: 5 tuples (1 block)

$s_D \Join F$

• $M = 9$ buffers at our disposal (1 is used for pipelining from selection)
• can't use one-pass join algorithm (not enough memory)
• sort-based join
  • note that $F$ is already sorted on F.did (it has a clustered index), so we need to sort only $s_D$
  • also output from selection of $E$ should be already sorted ($E$ has a clustering index on E.did), but normally we don't assume anything about the intermediate results - so we also calculate in the cost of sorting
  • cost: $2 B(s_D) \lceil \log_M B(s_D) \rceil + B(s_D) + B(F) = 2 \cdot 50 \cdot 2 + 50 + 37 = 287$
  • we can apply the optimization: $\left\lceil \cfrac{B(s_D)}{M} \right\rceil + 1 \leqslant M = 9$

  in this case the cost is:

  $2 B(s_D) [\lceil \log_M B(s_D) \rceil - 1] + B(s_D) + B(F) = 187$

• hash-based join
  • $k = \lceil \log_{M - 1} B(F) \rceil - 1 = 1$
  • cost: $2 \cdot B(s_D) \cdot k + 2 \cdot B(F) \cdot k + B(s_D) + B(F) = 2 \cdot 50 \cdot 1 + 2 \cdot 37 \cdot 1 + 50 + 37 = 261$
• index-join (using the clustered B-Tree on F.did)
  • cost: $B(s_D) + T(s_D) \times \left\lceil \cfrac{B(F)}{V(F, \text{did})} \right\rceil = 50 + 2500 \cdot \left\lceil \cfrac{37}{5000} \right\rceil = 2550$
• optimized sort-merge join is preferred

The best performing pair is $s_E \Join F$

• so we execute this join first
• and then join the results with $s_D$
• for that it's enough to have 2 memory buffers
  • one for pipelining $E$ from selection
  • another for one-pass join

Last join: $(s_E \Join F) \Join s_D$

• for $(s_E \Join F)$ we already use 2 buffers, therefore only 8 buffers left available
• one-pass join
  • cost: $B(s_E \Join F) + B(s_D) = 1 + 50 = 51$
• all other methods always cost more that one-pass join

The last projection also can be done on the fly - without materializing anything

Result

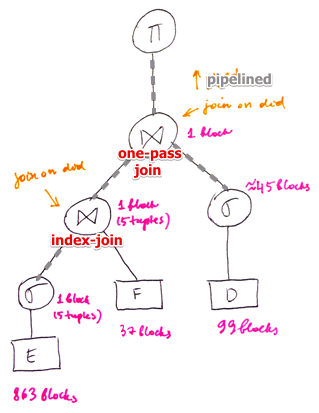
• note that we did not materialize anything:
• everything was done on the fly

See also

• Physical Operators (databases)
• Query Result Size Estimation
• Physical Query Plan Optimization
• Join Ordering
• B-Tree

Sources

• Database Systems Architecture (ULB)